diff --git a/README.md b/README.md
index 515ab24..51debc0 100644
--- a/README.md
+++ b/README.md
@@ -47,6 +47,8 @@ This is identical to (must be called in that order):
s.make_monotonic();
```
+
+
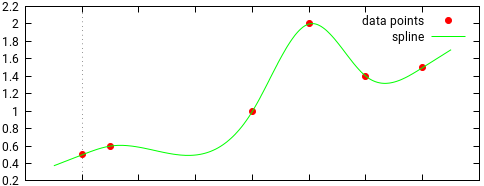
### Spline types
Splines are piecewise polynomial functions to interpolate points
(xi, yi). In particular, cubic splines can
diff --git a/doc/Makefile b/doc/Makefile
new file mode 100644
index 0000000..3059604
--- /dev/null
+++ b/doc/Makefile
@@ -0,0 +1,19 @@
+all: spline.pdf
+
+spline.pdf: spline.tex interpolate_avg.pdf positive_criteria.pdf spline.bbl spline.blg
+ pdflatex spline.tex
+
+interpolate_avg.pdf: interpolate_avg.gp
+ gnuplot interpolate_avg.gp
+
+positive_criteria.pdf: positive_criteria.gp
+ gnuplot positive_criteria.gp
+
+spline.bbl: literature.bib spline.tex
+ pdflatex spline; bibtex spline; pdflatex spline
+
+spline.blg: literature.bib spline.tex
+ pdflatex spline; bibtex spline; pdflatex spline
+
+clean:
+ rm -f *.pdf *.aux *.dvi *.log *.ps *.bbl *.blg
diff --git a/doc/README.md b/doc/README.md
new file mode 100644
index 0000000..67c0228
--- /dev/null
+++ b/doc/README.md
@@ -0,0 +1,12 @@
+## Spline documentation
+This contains the description of the mathematical background
+and is aimed at anyone who wants to understand the source code.
+
+### Prerequisites
+* [LaTex](https://www.latex-project.org/)
+* [Gnuplot](http://www.gnuplot.info/)
+
+### Building
+```
+$ make # builds spline.pdf
+```
diff --git a/doc/interpolate_avg.gp b/doc/interpolate_avg.gp
new file mode 100644
index 0000000..9a2e527
--- /dev/null
+++ b/doc/interpolate_avg.gp
@@ -0,0 +1,60 @@
+set term pdfcairo color solid size 12cm,8cm
+set output "interpolate_avg.pdf"
+
+# input points to interpolate (0,y1), (h,y2) with average avg
+h=1.0
+avg=1.0
+y1=4.0
+y2=2.0
+
+# calculate quadratic function: f(x) = a + b*x + c*x^2
+# which has the average avg and goes through both points
+a=y1
+b=2.0/h*(-2.0*y1-y2+3.0*avg)
+c=3.0/(h*h)*(y1+y2-2.0*avg)
+f(x) = a + b*x + c*x*x
+
+# make positive
+R=sqrt( (y1/avg)**2 + (y2/avg)**2 )
+if(R>3) {
+ z1=y1/R*3.0
+ z2=y2/R*3.0
+} else {
+ z1=y1
+ z2=y2
+}
+aa=z1
+bb=2.0/h*(-2.0*z1-z2+3.0*avg)
+cc=3.0/(h*h)*(z1+z2-2.0*avg)
+g(x) = aa + bb*x + cc*x*x
+
+#set size ratio -1
+set samples 300
+set colors classic
+set xzeroaxis
+set yzeroaxis
+set xrange [-0.05*h:1.05*h]
+
+set arrow from h, graph 0 to h,graph 1 nohead lt 0
+
+set arrow from 0,y1 to 0,z1 head lt 2 lw 1
+set arrow from h,y2 to h,z2 head lt 2 lw 1
+set label " =h" at h,screen 0.05
+set label " y_1" at 0,y1
+set label " y_2" at h,y2
+
+
+plot f(x) notitle with l lt 1 lw 1,\
+ g(x) notitle with l lt 2 lw 1 dt 2,\
+ avg notitle with l lt 0 lw 1,\
+ "-" using 1:(f($1)) notitle with p pt 7 lt 1,\
+ "-" using 1:(g($1)) notitle with p pt 7 lt 2
+0.0
+1.0
+e
+0.0
+1.0
+e
+
+
+pause -1
diff --git a/doc/literature.bib b/doc/literature.bib
new file mode 100644
index 0000000..7251b8d
--- /dev/null
+++ b/doc/literature.bib
@@ -0,0 +1,11 @@
+@STRING{SIAJN = {SIAM J. Numer. Anal.}}
+
+@article{Fri:1980:monotone_spline,
+ title={Monotone piecewise cubic interpolation},
+ author={Fritsch, F.N. and Carlson, R.E.},
+ journal=SIAJN,
+ volume={17},
+ number={2},
+ pages={238--246},
+ year={1980}
+}
diff --git a/doc/positive_criteria.gp b/doc/positive_criteria.gp
new file mode 100644
index 0000000..c1cf242
--- /dev/null
+++ b/doc/positive_criteria.gp
@@ -0,0 +1,27 @@
+set term pdfcairo color solid size 8cm,8cm
+set output "positive_criteria.pdf"
+
+
+# implicit equation: x^2+y^2+xy-6(x+y)+9=0
+f(x) = -0.5*(x-6.0) + sqrt( (-0.75*x+3.0)*x )
+g(x) = -0.5*(x-6.0) - sqrt( (-0.75*x+3.0)*x )
+
+# sufficient criteria: x^2+y^2=9
+h(x) = sqrt(9.0-x*x)
+
+
+set size ratio -1
+set samples 500
+set colors classic
+set xlabel "y_1"
+set ylabel "y_2"
+set xrange [0:4]
+
+set arrow from 0,0 to 0,3 nohead lt 1 lw 2
+
+plot f(x) title "exact" with l lt 1 lw 2,\
+ g(x)*(x>=3) notitle with l lt 1 lw 2,\
+ h(x)*(x<=3) title "sufficient" with l lt 2 dt 2
+
+
+pause -1
diff --git a/doc/spline.tex b/doc/spline.tex
new file mode 100644
index 0000000..78dbe8b
--- /dev/null
+++ b/doc/spline.tex
@@ -0,0 +1,518 @@
+\documentclass[11pt]{article}
+
+\usepackage{a4wide} % standard a4 margins
+\usepackage[pdftex]{graphicx} % options are: draft, dvips, pdftex
+\usepackage{theorem} % definition of new theorem environment
+\usepackage[sumlimits,nointlimits]{amsmath}
+\usepackage{amssymb,mathrsfs} % AMS symbols
+\usepackage{verbatim} % for comments
+\usepackage{textcomp} % degree symbol
+
+
+\parindent 0pt % no indent on new paragraphs
+\setlength{\parskip}{5pt plus 2pt minus 1pt} % distance btw. 2 paragraphs
+
+
+% my macros
+\newcommand{\R}{\mathbb{R}}
+\providecommand{\set}[1]{\left\{ #1 \right\}}
+\newcommand{\dd}{\:\text{d}}
+\newcommand{\avg}{\textit{avg}}
+\newcommand{\equivalent}{\Leftrightarrow}
+\newcommand{\follows}{\Rightarrow}
+\providecommand{\set}[1]{\left\{ #1 \right\}}
+\newcommand{\Co}{\mathrm{C}}
+\newcommand{\code}{\texttt}
+
+
+
+% -------------------- theorem environments ----------------------
+\theoremstyle{break} % main style for all theorems: plain, break
+\theoremheaderfont{\bf} % font used in the header
+{\theorembodyfont{\sl} % font used in the body
+ \newtheorem{theorem}{Theorem}[section]
+ \newtheorem{lemma}[theorem]{Lemma}
+ \newtheorem{corollary}[theorem]{Corollary}
+ \newtheorem{proposition}[theorem]{Proposition}
+ \newtheorem{assumption}[theorem]{Assumption}
+ \newtheorem{definition}[theorem]{Definition}
+}
+{\theorembodyfont{\rm}
+ \newtheorem{remark}[theorem]{Remark}
+ \newtheorem{example}[theorem]{Example}
+}
+\newenvironment{proof}{\par\noindent{\bf Proof~}
+ \ignorespaces}{\hspace*{\fill}~$\Box$\par\medskip}
+
+
+\def\parsedate #1:20#2#3#4#5#6#7#8\empty{20#2#3--#4#5--#6#7}
+\def\moddate#1{\expandafter\parsedate\pdffilemoddate{#1}\empty}
+
+\title{Cubic splines}
+\author{Tino Kluge}
+\date{\moddate{\jobname.tex}}
+%\date{\today}
+
+
+
+% -------------------- begin of document -------------------
+\begin{document}
+\maketitle
+
+\section{Interpolating cubic splines}
+\paragraph{Input:} a set of ordered $x, y$ coordinates\footnote{In this
+ document we start with index 1 which differs from C-convention
+ where indices start with 0. E.g.\ in this document $x_1$ equals to
+\code{x[0]} in code, $a_1=$ \code{a[0]}, $c_n=$ \code{c[n-1]}, etc.}
+\begin{equation*}
+\set{(x_1,y_1),\dots,(x_n,y_n)},\quad \text{with } x_1 < x_2 < \dots < x_n.
+\end{equation*}
+\paragraph{Output:} a piecewise cubic function
+\begin{equation}
+\begin{aligned}
+ f(x) & = \begin{cases}
+ f_0(x), & x0$. The interpolating function $f$
+as defined in Equation~\eqref{eq:interpolate_avg} then satisfies
+\begin{equation*}
+ f(x)\geq 0, \qquad \forall x\in[0,h],
+\end{equation*}
+if and only if
+\begin{equation}
+\label{eq:condition_non_negative}
+ z_1 + z_2 \leq 3 \quad \text{or} \quad
+ z_1^2 + z_2^2 + z_1 z_2 - 6 (z_1+z_2) + 9 \leq 0,
+\end{equation}
+with $z_1:=\frac{y_1}{\avg}$, $z_2:=\frac{y_2}{\avg}$. This is shown
+in red in Figure~\ref{fig:positive_criteria}. A sufficient but not
+necessary condition is
+\begin{equation}
+\label{eq:sufficient_condition_non_negative}
+ \sqrt{z_1^2+z_2^2} \leq 3 ,
+\end{equation}
+which is shown in green in Figure~\ref{fig:positive_criteria}.
+\end{proposition}
+\begin{proof}
+Note, if $c\neq 0$, $f$ has a local extrema $x^*$ at
+\begin{equation*}
+ x^* =-\frac{b}{2c}, \quad f(x^*) =a-\frac{b^2}{4c}.
+\end{equation*}
+Note also that the minimum of a function is either assumed on
+its boundaries or at a local minimum and we have assumed that on
+the boundary $f$ is non-negative ($y_1,y_2\geq 0$). Therefore,
+the function $f$ is non-negative in $[0,h]$ if and only if
+at least one of the following three criteria is satisfied:
+\begin{enumerate}
+ \item $f$ has no local minima, i.e. $c\leq 0$, and given
+ $c$ in Equation~\eqref{eq:avg_interp_solve_coeffs} this is equivalent
+ to
+ \begin{equation*}
+ \frac{y_1}{\avg} + \frac{y_2}{\avg} \leq 2.
+ \end{equation*}
+ \item $f$ has a local minima $x^*$ but $x^*\not\in (0,h)$
+ which is equivalent to $b\geq 0$ or $b\leq -2ch$
+ (since $c>0$). With $b$ and $c$ as given in
+ Equation~\eqref{eq:avg_interp_solve_coeffs}
+ this is equivalent to
+ \begin{equation*}
+ \frac{y_1}{\avg} + 2 \frac{y_2}{\avg} \leq 3 \quad \text{or} \quad
+ 2 \frac{y_1}{\avg} + \frac{y_2}{\avg} \leq 3.
+ \end{equation*}
+ \item \label{itm:minima_non_negative}
+ $f$ has a local minima but the minima is greater or equal zero,
+ i.e.\ $f(x^*)\geq 0$ which is equivalent to $a-\frac{b^2}{4c}\geq 0$
+ $\equivalent$ $4ac - b^2 \geq 0$, since $c>0$.
+ Given $a$, $b$ and $c$ as in Equation~\eqref{eq:avg_interp_solve_coeffs}
+ this is equivalent (after a little re-arranging) to
+ \begin{equation*}
+ \left(\frac{y_1}{\avg}\right)^2 +
+ \left(\frac{y_2}{\avg}\right)^2 +
+ \frac{y_1 y_2}{\avg^2}- 6 \frac{y_1+y_2}{\avg} + 9 \leq 0.
+ \end{equation*}
+\end{enumerate}
+$\dots$
+\end{proof}
+Note, the inequality under item
+\ref{itm:minima_non_negative} is the inside
+of an ellipse for $z_1:=\frac{y_1}{\avg}$ and $z_2:=\frac{y_2}{\avg}$,
+rotated by 90\textdegree\ and origin shifted to the coordinate $(2,2)$:
+\begin{itemize}
+\item Ellipse
+ \begin{equation*}
+ \frac{z_1^2}{6}+\frac{z_2^2}{2} = 1.
+ \end{equation*}
+\item Rotated\footnote{Rotation matrix
+ $A=\left(\begin{matrix}
+ \cos\varphi & \sin\varphi\\
+ -\sin\varphi &\cos\varphi\\
+ \end{matrix}\right)$
+ and inverse
+ $A^{-1}=\left(\begin{matrix}
+ \cos\varphi & -\sin\varphi\\
+ \sin\varphi &\cos\varphi\\
+ \end{matrix}\right)
+ = \sqrt{\frac{1}{2}}
+ \left(\begin{matrix}
+ 1 & -1 \\
+ 1 & 1 \\
+ \end{matrix}\right)$
+ for a 90\textdegree\ rotation. A set defined by an
+ implicit equation
+ $\set{x\in\R^2:g(x)=0}$ rotated is
+ $\set{Ax\in\R^2:g(x)=0}=\set{x\in\R^2:g(A^{-1}x)=0}$.
+ }
+ by 90\textdegree, i.e.
+ \begin{equation*}
+ \begin{split}
+ \frac{\frac{1}{2}(z_1-z_2)^2}{6}+\frac{\frac{1}{2}(z_1+z_2)^2}{2} & = 1,\\
+ & \Updownarrow\\
+ z_1^2 + z_2^2 + z_1 z_2 & = 3.
+ \end{split}
+ \end{equation*}
+\item Origin shifted to $(2,2)$, i.e.
+ \begin{equation*}
+ \begin{split}
+ (z_1-2)^2 + (z_2-2)^2 + (z_1-2) (z_2-2) & = 3,\\
+ & \Updownarrow\\
+ z_1^2 + z_2^2 + z_1 z_2 - 6(z_1+z_2) + 9 & = 0.
+ \end{split}
+ \end{equation*}
+\end{itemize}
+
+\begin{figure}
+ \centering
+ \includegraphics[width=0.50\textwidth]{positive_criteria}
+ \caption{Non-negativity of the interpolating function is guaranteed
+ if and only if $(y_1,y_2)$ are inside the red line
+ (in the case of $\avg=1$). A sufficient but not necessary
+ condition is drawn by the dashed green line.}
+ \label{fig:positive_criteria}
+\end{figure}
+
+% ----- bibliography -----
+\nocite{*}
+\bibliographystyle{plain}
+\bibliography{literature}
+
+
+
+\end{document}