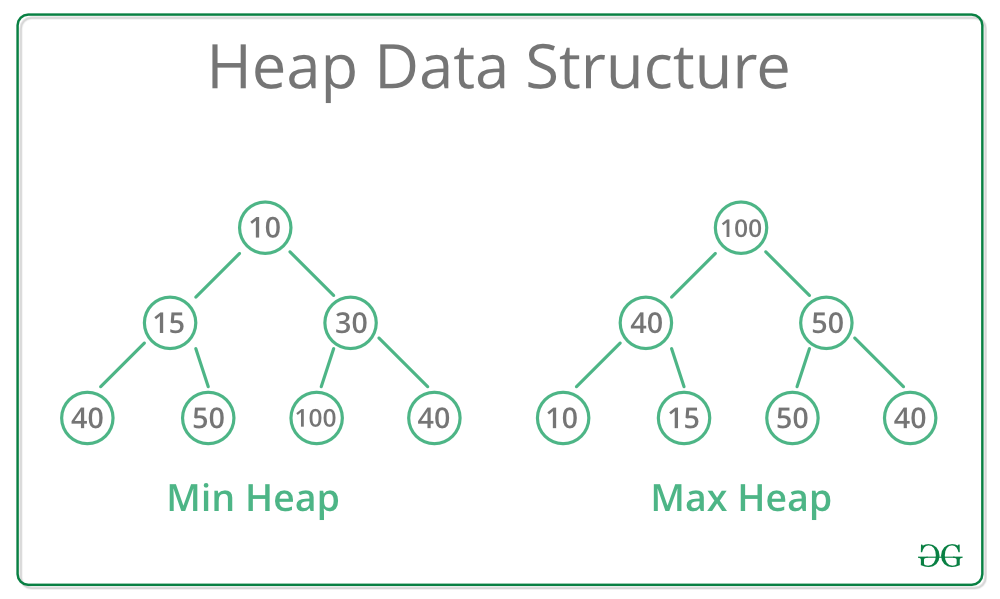
A heap is a complete binary tree that is usually stored in an array. The elements in a heap are organized as either a min heap or a max heap.
- Min Heap: The root element is the smallest, and each parent node is smaller than its children.
- Max Heap: The root element is the largest, and each parent node is larger than its children.
Heaps are best suited for implementing priority queues.
-
Binary Tree should be a Complete Binary Tree
A complete binary tree is a binary tree in which all the levels are completely filled except possibly for the last level, and the last level has all keys as left as possible.There should not be any blank spaces between the elements in an array. This structure is called a complete binary tree.
-
Node Relationships
- In a min heap, every node element should be greater than or equal to its descendants.
- In a max heap, every node element should be less than or equal to its descendants.
-
Creation: Build a heap by rearranging elements in an array to satisfy the heap properties.
Time Complexity: O(n log n) -
Insertion: Add a new element into the heap and ensure that the heap property is maintained.
Time Complexity: O(log n) -
Deletion: Remove the root (either the minimum or maximum, depending on heap type) and reheapify the structure.
Time Complexity: O(log n) -
Heapify: Adjusting an entire array into a heap structure.
Time Complexity: O(n)
Feel free to explore and contribute!