- ওয়ান হট এনকোডিং (One Hot Encoding) / 1-K Class Representation
- মাল্টিনোমিয়াল ডিস্ট্রিবিউশন ও Softmax ফাংশনের উৎপত্তি
- মাল্টিক্লাস লগ লাইকলিহুড
- সফটম্যাক্স ও এর ডেরিভেটিভ
- ক্যাটেগরিক্যাল ক্রস-এন্ট্রপি ও এর ডেরিভেটিভ
শেষ অধ্যায়ে আমরা দেখেছিলাম কীভাবে একটি লজিস্টিক রিগ্রেশন মডেল স্ক্র্যাচ থেকে তৈরি করা যায়। একইভাবে আমরা NumPy ব্যবহার করে আজকেও একটা ক্লাসিফায়ার তৈরি করব যেটা Digit Recognize করতে পারে। তবে সেটা তৈরি করার আগে আমাদের অতিরিক্ত কিছু বিষয় সম্পর্কে ধারণা রাখতে হবে।
এখানে কিঞ্চিৎ সমস্যার উদ্ভব হয়েছে। কারণ, দুইটা ক্লাসের ক্ষেত্রে আমরা 0 বা 1 দিয়ে রিপ্রেজেন্ট করলেই পারতাম। এবং সিগময়েডের রেঞ্জ [0, 1] পর্যন্তই ছিল। এখন আমরা যদি এই তিনটা ক্লাস কে 0, 1 এবং 2 দ্বারা রিপ্রেজেন্ট করি তাহলে তৃতীয় ক্লাস বের করব কীভাবে মডেল থেকে? আমাদের নতুন কোন সিগময়েড ফাংশন বানাতে হবে যার রেঞ্জ [0, 2]?
এই সমস্যা দূর করার জন্য এবং Multinomial Distribution ঠিক রাখার জন্য আমরা নিচের মত করে রিপ্রেজেন্ট করব।
এটাকেই আমরা 1-K Class Representation বা One Hot Encoding বলব।
ম্যাথের ভাষায়, এই রিপ্রেজেন্টেশনের ডিমেনশন হবে এরকম। $$ C \in \mathbb{R}^{D \times 1} \ \text{Where, } D = \text{Number of Classes} \ $$
GLM এর মাধ্যমে পূর্বে Logistic Regression এর ক্ষেত্রে Bernoulli Distribution, Exponential Family এর দ্বারা Sigmoid এর প্রমাণ আমরা দেখেছিলাম। বাইনারি ক্লাস আসে Bernoulli Distribution থেকে, একইভাবে মাল্টিক্লাস আসে Multinomial Distribution থেকে। ন্যাচারাল প্যারামিটার
Multinomial Data এর ক্ষেত্রে GLM ডিরাইভ করতে হবে। প্রথমে Multinomial Distribution কে Exponential Family তে রিপ্রেজেন্ট করব যাতে করে আমরা Natural Parameter এর এক্সপ্রেশন পাই।
বাইনোমিয়াল ডিস্ট্রিবিউশনের ক্ষেত্রে, একটা নির্দিষ্ট আউটকাম (কয়েন টস এর জন্য Head/Tail) বের করতে হলে, একটা প্যারামিটারের মান বের করলেই হত, কারণ আরেকটা আউটকামের প্রব্যাবিলিটি
তাহলে, প্রতিটা আউটকাম এর রেজাল্ট এমন হতে হবে, যেন আবার তাদের যোগফল 1 হয়। প্রব্যাবিলিটির সূত্রানুযায়ী।
যদি আবহাওয়া এর অবস্থা বিবেচনায় আনি, $$ P(\text{Rain}) = 0.3 \ P(\text{Sunny}) = 0.5 \ P(\text{Snow}) = ? $$ এটা বের করা খুবই সহজ, $$ \begin{align} P(\text{Snow}) &= 1 - { P(\text{Rain}) + P(\text{Sunny}) } \ &= 1 - (0.3 + 0.5) \ &= 0.2 \end{align} $$ একে এখন সাধারণ ফর্মে লিখতে হবে,
ধরি
,
T(k) = \begin{bmatrix}
0 \
0 \
0 \
\vdots \
1
\end{bmatrix}
$$
তাই, $$i-$$th এলিমেন্ট কে রিপ্রেজেন্ট করার জন্য একে,
ইন্ডিকেটর ফাংশন একটা আর্গুমেন্ট নেয় যদি সেটা সত্য হয় তাহলে সে 1 না 0।
$$
(T(y))_{i} = 1 { y=i }
$$
বার্নুলির ক্ষেত্রে লিখতাম, $$ p(y; \phi) = \phi^{y}(1-\phi)^{1-y} $$ Multinomial Distribution এর ক্ষেত্রে লিখতে হবে, $$ \begin{align} p(y;\phi) &= \phi_{1}^{1 { y=1 }} \phi_{2}^{1 { y=2 }} \dots \phi_{k}^{1 { y=k }} \ &= \phi_{1}^{1 { y=1 }} \phi_{2}^{1 { y=2 }} \dots \phi_{k}^{ 1 - \sum_{i=1}^{k-1} 1{y=i} } \ &= \phi_{1}^{(T(y)){1}} \phi{2}^{(T(y)){2}} \dots \phi{k}^{ 1 - \sum_{i=1}^{k-1} (T(y))_{i} } \
&= \exp \left( (T(y)){1} \log\phi{1} + (T(y)){2} \log\phi{2} + \dots + \left( 1 - \sum_{i=1}^{k-1} (T(y)){i} \right) (T(y)){k} \log\phi_{k} \right) \
&= \exp \left( (T(y)){1} \log{ \frac{ \phi{i} } { \phi_{k} } } + (T(y)){2} \log{ \frac{ \phi{2} } { \phi_{k} } } + \dots + (T(y)){k-1} \log{ \frac{\phi{k - 1} }{ \phi_{k} } + \log{\phi_{k}} } \right) \
&= b(y) \exp { \left( \eta^{T} T(y) - a(\eta) \right) } \end{align} $$ যেখানে, $$ \eta = \begin{bmatrix} \log \left(\frac{\phi_{1}}{\phi_{k}} \right) \ \log \left(\frac{\phi_{2}}{\phi_{k}} \right) \ \vdots \ \log \left(\frac{\phi_{k-1}}{\phi_{k}} \right) \ \end{bmatrix} $$
সুতরাং, $$ \begin{align}
\eta_{i} &= \log { \frac{\phi_{i}} {\phi_{k}} } \
e^{ \eta_{i} } &= \frac{\phi_{i}} {\phi_{k}} \
\phi_{k}e^{\eta_{i}} &= \phi_{i} \
\phi_{k} \sum_{i=1}^{k} e^{\eta_{i}} &= \sum_{i=1}^{k}\phi_{i} \
\phi_{k} &= \frac{1}{ \sum_{i=1}^{k} e^{\eta_{i}} }
\end{align}
$$
উপরের গ্রুপের দ্বিতীয় সমীকরণে
লিনিয়ার মডেলের প্যারামিটার যদি
যদি ডিজিটের ইমেজ ডেটা আমাদের কাছে থাকে, আর প্রতিটি ইমেজ $$ 2 \times 2$$ পিক্সেল হয় তাহলে
তাহলে এক্সপেক্টশন, $$ \begin{align} p(y = i | x;W) &= \phi_{i} \ &=\frac{ e^{ \eta_{i} } }{ \sum_{i=1}^{k} e^{\eta_{i}} } \
&=\frac{ e^{ W_{i}^{\top}x } }{ \sum_{i=1}^{k} e^{W_{i}^{ \top }x } } \end{align} $$
Multinomial Distribution এর লগ লাইকলিহুড এর নেগেটিভ-ই হল ক্যাটেগরিকাল ক্রসএন্ট্রপি লস ফাংশন।
বাইনোমিয়ালের মতই এর লগ লাইকলিহুড এরকম, [Ref: Machine Learning : Probabilistic Perspective by Murphy P-253]
একত্রে,
লিনিয়ার মডেল (Linear Model), সফটম্যাক্স অ্যাক্টিভেশন (Softmax) ও ক্যাটেগরিক্যাল ক্রসএন্ট্রপি (Categorical Cross-entropy)
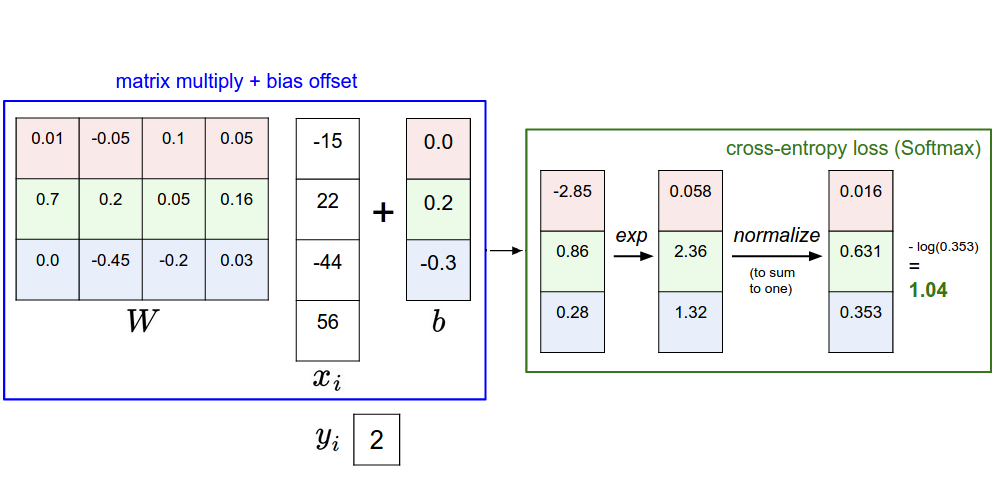
আমরা এতক্ষণ ধরে বিভিন্ন ফাংশনের ম্যাথেমেটিক্যাল রূপ দেখলাম। এবার একটু ভিজুয়ালি বুঝার চেষ্টা করব। নিচের রিসোর্সগুলি এখান থেকে কালেক্টেড।
এখানে দেখা যাচ্ছে, ইনপুট ইমেজ কে একটা Weight Matrix এর সাথে ম্যাট্রিক্স মাল্টিপ্লিকেশন করা হচ্ছে এবং তার স্কোর ডিফাইন করা হচ্ছে। এই অপারেশন টা হল,
এখানে আমরা তিনটা স্কোর পাচ্ছি, কিন্তু মাল্টিক্লাস রিগ্রেশনের ক্ষেত্রে একে অবশ্যই Probability তে কনভার্ট করতে হবে। আর সেটার জন্য আমরা জানি Softmax অ্যাপ্লাই করলেই হবে।
এখানে দেখতে পাচ্ছি Dog score বেশি দিচ্ছে, Cat score এর তুলনায়। আমাদের Objective হল Weight Matrix এর মান এমন হতে হবে, যেন এটি Cat image এর জন্য High score দেয় এবং বাকি ক্লাসের জন্য Low score দেয়, তেমনি Dog এর ক্ষেত্রে শুধু Dog এ High Score দিবে এবং বাকিদের Low score দিবে।
ধরা যাক একটা Ship ইমেজ লিনিয়ার মডেলে ফিড করলাম, তাতে মান আসল, Cat Score: 50.0, Dog Score: -20 এবং Ship Score: 60।
এখন এর উপরে সফটম্যাক্স চালালে মান আসবে যথাক্রমে,
Cat Probability: 0.0000453
Dog Probability: 0.0000000000000000.....
Ship Probability: 0.9999
তারমানে, $$ P( y^{(i)} = k |x^{(i)},W) = \text{softmax} (Wx^{(i)}) $$
- একটা র্যান্ডম Weight ম্যাট্রিক্স ইনিশিয়ালাইজ করে প্রেডিকশন চালাতে হবে
- ক্যাটেগরিক্যাল ক্রসএন্ট্রপি লস ক্যালকুলেট করতে হবে
-
$$W$$ এর সাপেক্ষে$$\mathcal{L}(y, \hat{y})$$ এর গ্রেডিয়েন্ট বের করতে হবে, $$ \nabla_{W} \mathcal{L(y, \hat{y})} $$ - নতুন
$$W$$ হবে আগের$$W$$ থেকে$$\text{learning rate} \times \nabla_{W} \mathcal{L(y, \hat{y})} $$ কম বা Weight Update Rule:- $$ W := W - \alpha \times \nabla_{W} \mathcal{L(y, \hat{y})} $$
- পরবর্তী ইটারেশনে আবার লস ক্যালকুলেট করে দেখতে হবে লস কমেছে কিনা, যতক্ষণ না কনভার্জ হচ্ছে ততক্ষণ ইটারেট করতে হবে।
দ্রষ্টব্য, সবকিছুই ভেক্টরাইজড ইম্প্লিমেন্টেশন করব
- আউটপুট ভ্যালু One Hot Encoding এ এনকোড করতে হবে
- Softmax ইম্প্লিমেন্ট করতে হবে
- Predict ফাংশন তৈরি করতে হবে
- ক্রস-এন্ট্রপি লস ইম্প্লিমেন্ট করতে হবে
- গ্রেডিয়েন্ট ক্যালকুলেট করতে হবে তারপর ইম্প্লিমেন্ট করতে হবে
- সবশেষে মডেল ট্রেইন করে কনফিউশন ম্যাট্রিক্স জেনারেট করতে হবে ও Weight ভিজ্যুয়ালাইজ করতে হবে
def to_categorical(y, num_class=10):
return np.eye(num_class)[y]টেস্ট
In [69]: to_categorical(5)
Out[69]: array([ 0., 0., 0., 0., 0., 1., 0., 0., 0., 0.])
In [71]: to_categorical([0, 1, 2, 9])
Out[71]:
array([[ 1., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[ 0., 1., 0., 0., 0., 0., 0., 0., 0., 0.],
[ 0., 0., 1., 0., 0., 0., 0., 0., 0., 0.],
[ 0., 0., 0., 0., 0., 0., 0., 0., 0., 1.]])সফটম্যাক্সের সমীকরণ হল এটা,
# I won't rewrite this dependency again
import numpy as np
def softmax(X):
return np.exp(X) / np.sum(np.exp(X))এই ইম্প্লিমেন্টেশনে কিছু সমস্যা আছে, যেমন
In [29]: softmax(np.array([123, 456, 789]))
RuntimeWarning: overflow encountered in exp
RuntimeWarning: invalid value encountered in true_divide
Out[29]: array([ 0., 0., nan])
তাহলে এইরকম Numerical Unstability যাতে না হয় সেকারণে আমাদের এক্স্ট্রা কিছু স্টেপ নিতে হবে।
def softmax(X):
# Getting max scores from each row then reshaping in a way that we can subtract the values via broadcasting
max_probabilities = np.max(X, axis=1).reshape((-1, 1))
# Subtracting from max value [Normalization trick]
X -= max_probabilities
# Performing exp
np.exp(X, out=X)
# Denominator
sum_probabilities = np.sum(X, axis=1).reshape((-1, 1))
# Dividing
X /= sum_probabilities
return Xটেস্ট করা যাক,
ধরি, দুইটা ইমেজ লিনিয়ার মডেলে ফিড করলাম, তাতে ক্লাসংখ্যা যদি ৩ হয় (ধরি, কুকুর, বিড়াল আর পাখি) তাহলে প্রতি ছবির জন্য ৩ সেট করে স্কোর পাব।
তাহলে, দুইটা ইমেজের জন্য মোট ৬ টা স্কোর। প্রথম ইমেজের Cat Score, Dog Score, Bird Score, আবার দ্বিতীয় ইমেজের জন্য Cat score, Dog score, Bird Score ।
In [53]: X = np.array([[123.0, 456.0, 789.0], [1122.0, 3344.0, 5566.0]])
In [54]: X
Out[54]:
array([[ 123., 456., 789.],
[ 1122., 3344., 5566.]])
In [55]: softmax(X)
Out[55]:
array([[ 5.75274406e-290, 2.39848787e-145, 1.00000000e+000],
[ 0.00000000e+000, 0.00000000e+000, 1.00000000e+000]])
# Finding the the classes using argmax
In [67]: np.argmax(softmax(X), axis=1)
Out[67]: array([2, 2], dtype=int64)প্রেডিকশন হল, ইনপুট ডেটা ও ওয়েট ম্যাট্রিক্সের ডট প্রোডাক্টের softmax
$$
P( y^{(i)} = k |x^{(i)},W) = \text{softmax} (Wx^{(i)})
$$
def predict(X, W):
return softmax(X.dot(W.T))Cross Entropy এর সমীকরণ এটা,
টেস্ট করা যাক,
In [64]: y_pred = np.array([[ 0., 0., 0., 1., 0., 0., 0., 0., 0., 0.]])
In [65]: y_true = np.array([[ 0., 0., 1., 0., 0., 0., 0., 0., 0., 0.]])
In [66]: categorical_crossentropy(y_true, y_pred)
Out[66]: 2.3025850929940455গ্রেডিয়েন্ট কম্পিউট করা কঠিনতম কাজগুলার মধ্য়ে একটি। কম্পিউট করার আগে স্পয়লার দেয়া যাক। আর এই অধ্যায়ের শেষের দিকে প্রমাণ দিয়ে দেব।
# Here y_true and y_pred are one hot encoded
def compute_gradient(X, y_true, y_pred):
return (y_pred - y_true).T.dot(X)গ্রেডিয়েন্ট ডিসেন্টের ফরমূলা থেকে জানি, $$ W := W - \alpha \times \nabla_{W} \mathcal{L(y, \hat{y})} $$
def update_weights(W, dW, learning_rate=0.01):
assert W.shape == dW.shape
W = W - learning_rate * dW
return Wএখানে আমরা ব্যবহার করব sklearn এর digit dataset।
import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import load_digits
x, y = load_digits(return_X_y=True)
num_class = 10
num_features = x.shape[1]
iterations = 100
iters = []
costs = []
# Init weights
W = np.zeros((num_class, num_features))
y = to_categorical(y)
for i in range(iterations):
# prediction
y_pred = predict(x, W)
# calculating cost
cost = categorical_crossentropy(y, y_pred)
print("Cost {}".format(cost))
# computing gradient
dW = compute_gradient(x, y, y_pred)
# updating the weights via batch gradient descent
W = update_weights(W, dW)
# saving the costs for plotting
iters.append(i)
costs.append(cost)আউটপুট
Cost 2.302585092994046
Cost 0.2670943780065689
Cost 1.7390908808458307
Cost 1.0858295932813709
Cost 1.3609315784647058
Cost 1.7029135254469814
Cost 1.5824804028514838
Cost 1.0676739238351907
Cost 1.3941423500093804
....
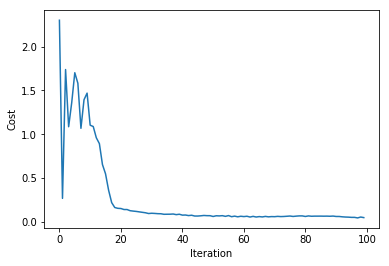
plt.xlabel('Iteration')
plt.ylabel('Cost')
plt.plot(iters, costs)sklearn এর confusion_matrix ব্যবহার করে ও matplotlib এর মাধ্যমে প্লট করব।
from sklearn.metrics import confusion_matrix
import itertools
# http://scikit-learn.org/stable/auto_examples/model_selection/plot_confusion_matrix.html#sphx-glr-auto-examples-model-selection-plot-confusion-matrix-py
def plot_confusion_matrix(cm, classes,
normalize=False,
title='Confusion matrix',
cmap=plt.cm.Blues):
"""
This function prints and plots the confusion matrix.
Normalization can be applied by setting `normalize=True`.
"""
if normalize:
cm = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis]
print("Normalized confusion matrix")
else:
print('Confusion matrix, without normalization')
print(cm)
plt.imshow(cm, interpolation='nearest', cmap=cmap)
plt.title(title)
plt.colorbar()
tick_marks = np.arange(len(classes))
plt.xticks(tick_marks, classes, rotation=45)
plt.yticks(tick_marks, classes)
fmt = '.2f' if normalize else 'd'
thresh = cm.max() / 2.
for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
plt.text(j, i, format(cm[i, j], fmt),
horizontalalignment="center",
color="white" if cm[i, j] > thresh else "black")
plt.tight_layout()
plt.ylabel('True label')
plt.xlabel('Predicted label')
# Compute confusion matrix
y_true = np.argmax(y, axis=1)
y_pred = np.argmax( predict(x, W), axis=1 )
cnf_matrix = confusion_matrix(y_true, y_pred)
plot_confusion_matrix(cnf_matrix, classes="0 1 2 3 4 5 6 7 8 9".split())কনফিউশন ম্যাট্রিক্স প্লট
এখানে আমি Weight এর ইমেজ ভাল বোঝার জন্য রিসাইজ করে 20x20 করব।
plt.imshow(cv2.resize(W[0, :].reshape(8, 8), (20, 20)), cmap='gray')plt.imshow(cv2.resize(W[1, :].reshape(8, 8), (20, 20)), cmap='gray')plt.imshow(cv2.resize(W[2, :].reshape(8, 8), (20, 20)), cmap='gray')plt.imshow(cv2.resize(W[3, :].reshape(8, 8), (20, 20)), cmap='gray')plt.imshow(cv2.resize(W[4, :].reshape(8, 8), (20, 20)), cmap='gray')plt.imshow(cv2.resize(W[5, :].reshape(8, 8), (20, 20)), cmap='gray')plt.imshow(cv2.resize(W[6, :].reshape(8, 8), (20, 20)), cmap='gray')plt.imshow(cv2.resize(W[7, :].reshape(8, 8), (20, 20)), cmap='gray')plt.imshow(cv2.resize(W[8, :].reshape(8, 8), (20, 20)), cmap='gray')plt.imshow(cv2.resize(W[9, :].reshape(8, 8), (20, 20)), cmap='gray')দেখা যাচ্ছে ট্রেইনিং শেষে Weight এর মানগুলো এমন আসছে যে এটা একটি টেম্প্লেট বানিয়ে ফেলেছে।
আমরা প্রায় শেষের দিকে, এখন প্রমাণ করব Cross-entropy ও Softmax এর জন্য গ্রেডিয়েন্ট ওইরকম আসল কীভাবে।
ধরি,
$$
Z = WX \
\frac{ \partial Z}{\partial W} = X
$$
পার্শিয়াল ডেরিভেটিভ এর চেইন রুল অনুযায়ী,
$$
\frac{ \partial \mathcal{L} (y, \hat{y}) }{\partial W} = \frac{ \partial \mathcal{L} (y, \hat{y}) }{\partial Z} . \frac{ \partial Z }{ \partial W }
$$
এখন
- \sum_{j=1}^C y_j \frac{\partial log(\hat{y}j)}{\partial Z_i} \ &= - \sum{j=1}^C y_j \frac{1}{ \hat{y}_j } \frac{\partial \hat{y}_j}{\partial Z_i} \
&= - \frac{y_i}{\hat{y}_j} \frac{\partial \hat{y}j}{\partial Z_i} - \sum{j \neq i}^C \frac{y_j}{\hat{y}_j} \frac{\partial \hat{y}_j}{\partial Z_i} \
&= - \frac{y_i}{\hat{y}_j} \hat{y}_j (1-\hat{y}j) - \sum{j \neq i}^C \frac{y_j}{\hat{y}_j} (-\hat{y}_i \hat{y}_j) \
&= - y_i + y_i \hat{y}i + \sum{j \neq i}^C y_j \hat{y}i = - y_i + \sum{j = 1}^C y_j \hat{y}_i \
&= -y_i + \hat{y}i \sum{j = 1}^C y_j \
&= \hat{y}_i - y_i \
\end{align}
$$
এখানে,
$$\frac{\partial \hat{y}_j}{\partial Z_i} $$ এর মান দুইরকম হওয়ার কারণ কী? সেটার প্রমাণ দেখে নেয়া যাক, $$ \begin{split} \text{if} ; i = j :& \frac{\partial \hat{y}_i}{\partial Z_i} = \frac{\partial \frac{e^{Z_i}}{\Sigma_C}}{\partial Z_i} = \frac{e^{Z_i}\Sigma_C - e^{Z_i}e^{Z_i}}{\Sigma_C^2} = \frac{e^{Z_i}}{\Sigma_C}\frac{\Sigma_C - e^{Z_i}}{\Sigma_C} = \frac{e^{Z_i}}{\Sigma_C}(1-\frac{e^{Z_i}}{\Sigma_C}) = \hat{y}_i (1 - \hat{y}_i ) \
\text{if} ; i \neq j :& \frac{\partial \hat{y}_i}{\partial Z_j} = \frac{\partial \frac{e^{Z_i}}{\Sigma_C}}{\partial Z_j} = \frac{0 - e^{Z_i}e^{Z_j}}{\Sigma_C^2} = -\frac{e^{Z_i}}{\Sigma_C} \frac{e^{Z_j}}{\Sigma_C} = -\hat{y}_i \hat{y}_j \end{split} $$ সবশেষে, $$ \frac{ \partial \mathcal{L} (y, \hat{y}) }{\partial W} = \frac{ \partial \mathcal{L} (y, \hat{y}) }{\partial Z} . \frac{ \partial Z }{ \partial W } \ = (\hat{Y} - Y) \times X $$ (ম্যাট্রিক্স ফরম্যাটে)
এটাই হল সেই গ্রেডিয়েন্ট যেটা আমরা উপরে ইম্প্লিমেন্ট করি।
- Bias অ্যাড করতে পারেন
- এখানে ভেক্টরাইজড ইম্প্লিমেন্টেশন দেখানো হয়েছে। আপনারা লুপের সাহায্যে ইম্প্লিমেন্ট করে দেখতে পারেন একই রেজাল্ট আসছে কিনা।