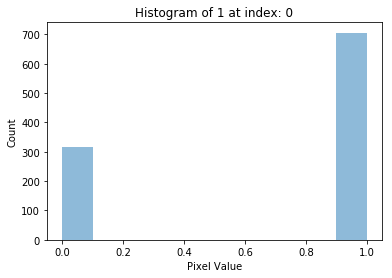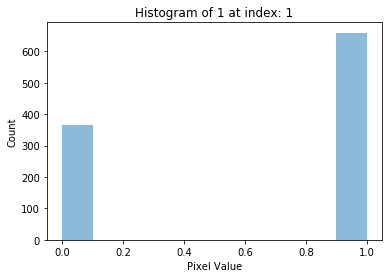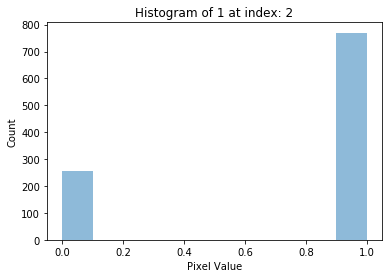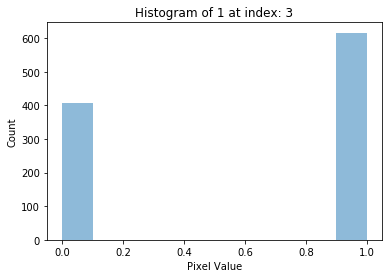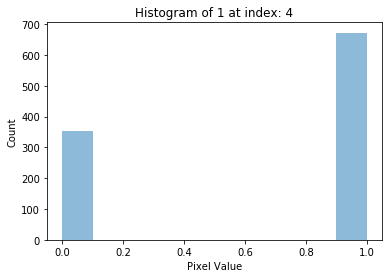সব্জির বাটিটা ফেলুদা হাতে নিয়ে বলল, "যারা যারা খুন হয়েছেন, তারা প্রত্যেকেই প্রত্যক্ষ বা পরোক্ষভাবে ওপেনসোর্স অ্যাক্টিভিটির সাথে জড়িত।"
বললাম, "সেটা বুঝলে কী করে?"
-"ওরে বোকচন্দর, সেটা তো একটু গুগল আর ফিল্ডওয়ার্ক করলেই বোঝা যায়। তোকে যে কাজ দিয়েছিলাম তার কী খবর?"
-"আমার মনে হয় কাজটা অনেক জটিল, আমার মাথায় কিছু আইডিয়া এসেছে, সেগুলো একটু প্রয়োগ করে দেখবখন।"
-"তা করিস, আর মাথায় রাখিস কাজটা খুবই দ্রুত করতে হবে, সিধু জ্যাঠার সাথেও একটু আলোচনা করতে এটা নিয়ে। দেখি উনি কিছু আলোকপাত করতে পারেন কিনা।"
এরপর আর তেমন কোন কথা হল না, খাওয়া শেষ করে নিজের রুমে ফিরে গিয়ে কম্পিউটার চালু করে ফাইলগুলো ওপেন করলাম।
যে কাজটা করব ভেবেছিলাম সেটা দিয়েই শুরু করা উচিৎ বলে মনে হল। এখানে একটু বলে রাখা দরকার, আমি ছবিগুলো সব বাইনারি লেভেলে নিয়ে আসব rgb2gray ফাংশনের মাধ্যমে, মানে কালো পিক্সেলগুলোর নিউমেরিকাল ভ্যালু $$ 1 $$ এবং সাদাগুলোর $$ 0 $$ । এই দুই মান ছাড়া অন্য কোন মানের পিক্সেল ছবিতে থাকবে না।
প্রথমে যেটা করা দরকার, আরও কিছু হেল্পার ফাংশন লিখতে হবে যেটা দিয়ে আমি প্লটিং আর কাউন্টিংয়ের কাজ সহজেই করতে পারব।
import matplotlib.image as mpimg
# Plots histogram of a given digit
def plot_hist(digit, index):
data = rgb2gray(mpimg.imread(load_digit(digit)[index])).ravel()
plt.hist(data, alpha=0.5)
plt.title("Histogram of " + str(digit) + " at index: " + str(index))
plt.xlabel("Pixel Value")
plt.ylabel("Count")
plt.show()এই ফাংশনের সাহায্যে আমি যেকোন ডিজিটের হিস্টোগ্রাম প্লট করতে পারব। এর আগে একটু হিস্টোগ্রাম সম্পর্কে বলি। হিস্টোগ্রাম হচ্ছে একটা রেঞ্জের মধ্যে একটা ভ্যালু কতবার আছে তার বার প্লট।
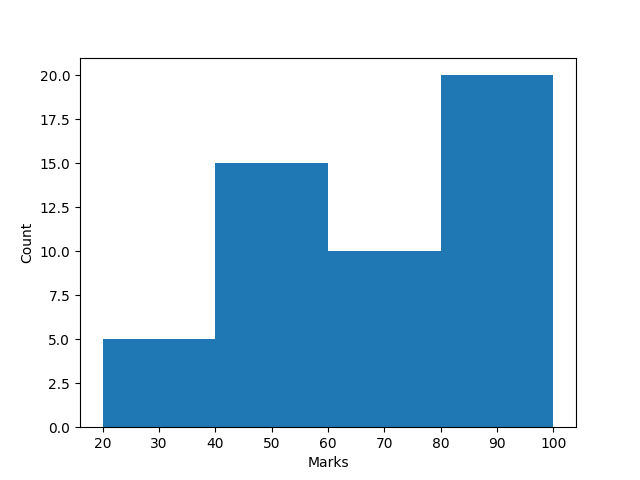
ধরি আমি একজন স্কুলশিক্ষক এবং আমি আমার $$ 50 $$ জন ছাত্রদের গণিত বিষয়ের নম্বরের হিস্টোগ্রাম প্লট করতে চাচ্ছি। তাহলে আমি প্রথমেই যে কাজটা করব সেটা হচ্ছে পরীক্ষায় সর্বোচ্চ নম্বর $$ 100 $$ কে আমি কতগুলো রেঞ্জে ভাগ করব। হিসাবের সুবিধার্থে আমি $$ 100 $$ কে $$ 5 $$ ভাগ করি তাহলে প্রতিভাগে রেঞ্জ হবে অনেকটা এরকম $$ 0 - 20 , 21 - 40, 41 - 56, 61 - 80, 81 - 100 $$
এই যে আমি কতগুলা রেঞ্জে ক্যাটাগরি করলাম এগুলোকে বলে এক একটা bin
এরপর আমি হিসাব করব, $$ 0-20 $$ মার্ক পেয়েছে এমন কতজন ছাত্র আছে, $$ 21-40 $$ মার্ক পেয়েছে এমন কতজন আছে এভাবে একটি ডেটা টেবিল তৈরি করব।
নিচের সাজানো ডেটাটেবিল পাইথনে অটোমেটিক তৈরি করা যায় শুধু
histফাংশন কল করার মাধ্যমে।
20, 20, 20, 20, 20,
40, 40, 40, 40, 40, 40, 40, 40, 40, 40, 40, 40, 40, 40, 40,
60, 60, 60, 60, 60, 60, 60, 60, 60, 60,
80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80,
100, 100, 100, 100, 100
| Bins of Mark (প্রাপ্ত নম্বর) | Count (কতজন পেয়েছে) |
|---|---|
| $$ 0 - 20 $$ | $$ 5 $$ |
| $$ 21-40 $$ | $$ 15 $$ |
| $$ 41-60 $$ | $$ 10 $$ |
| $$ 61-80 $$ | $$ 15 $$ |
| $$ 81-100 $$ | $$ 5 $$ |
# Plotting histogram of the above data table
data = np.array([20, 20, 20, 20, 20, 40, 40, 40, 40, 40, 40, 40, 40, 40, 40, 40, 40, 40, 40, 40, 60, 60, 60, 60, 60, 60, 60, 60, 60, 60, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 100, 100, 100, 100, 100])
# For simplicity, bin starts from 20 upto 100 and the width of a bin is 20
bins = np.arange(20, 120, 20)
plt.hist(data, bins=bins)
plt.show()আমাদের ইমেজে আছেই দুইরকমের মান, একটি হল $$ 0 $$ আরেকটি হল $$ 1 $$ । সেক্ষেত্রে হিস্টোগ্রাম আসবে দুইটা বার কিন্তু তাদের হাইট কত হবে সেটা নির্ভর করবে $$ 0 $$ বা $$ 1 $$ কতবার আছে তার উপর।
একটা ইমেজের হিস্টোগ্রাম বের করা দেখা যাক আমার তৈরিকৃত ফাংশন দিয়ে।
আমি এখন '১' এর যতগুলো ছবি আছে তাদের লিস্টের প্রথম ছবিটার হিস্টোগ্রাম প্লট করব নিচের কোড দিয়ে।
# Plotting histogram of digit 1 from index 0
plot_hist(1, 0)এখন দেখতে হবে প্রতিটা ডিজিটের হিস্টোগ্রাম কতটা আলাদা হয়, কারণ তাহলে আমি একটা থ্রেসহোল্ডিং বসাতে পারব যে $$ ০ $$ পিক্সেল ভ্যালু এর সংখ্যা বা $$ ১ $$ পিক্সেল ভ্যালু এর সংখ্যা এতগুলো হলে সেটা $$ ১, ২, ৩ .. $$ ইত্যাদি ডিজিট হবে।
দুইটা ডিজিট যদি আমি চিনতে চাই তাহলে তাদের মধ্যে এমন একটা সাধারণ বৈশিষ্ট্য থাকবে যেটার মাধ্যমে আমি আলাদা করতে পারব। যেমন হতে পারে কতগুলো কালো/সাদা পিক্সেল প্রতি ইমেজে আছে। যদি আমি দেখি যে ১ এর ক্ষেত্রে কালো পিক্সেলের সংখ্যা ২ এর তুলনায় ৫০ টা বেশি থাকে তাহলে আমি বলতে দুইটা ইমেজ তুলনা করে বলে দিতে পারব কোনটা ১ এবং কোনটা ২।
সংখ্যাগত তুলনায় যাওয়ার আগে ভিজুয়াল কম্প্যারিজনের বিষয়টা মনে ধরল। তাই সংখ্যা ১ এর কয়েকটা স্যাম্পলের হিস্টোগ্রাম প্লট করে দেখব কোন প্যাটার্ন পাওয়া যায় কিনা।
# Plotting histogram of five instances of digit 1
for i in range(5):
plot_hist(1, i)চারটা হিস্টোগ্রাম প্লট পেলাম,
এখানে একই সংখ্যার বিভিন্ন স্যাম্পলের হিস্টোগ্রাম প্লট করলাম। আশানুরূপ ফলাফল পাচ্ছি না কারণ সাদা ও কালোর পিক্সেল সংখ্যার কোন নির্দিষ্ট মান নেই!
এই তুলনা করার আগে আমার দেখতে হবে আমি যে ভিত্তিতে আগাচ্ছি সেটা কাজ করবে কিনা। তাই আমার অনেকগুলো স্যাম্পল নিয়ে আমার ধারণা প্রয়োগ করে দেখতে হবে আমি কতটা ঠিক বা ভুল। আমি ১ ও ২ এর থেকে প্রতি ডিজিটের ১০০ টি করে ইমেজ নিয়ে গড় করে দেখব ১ ও ২ সংখ্যায় কালো ও সাদা পিক্সেল কতগুলো আছে। যদি একটা বিশাল পার্থক্য পাই তাহলে খুব সহজেই আমি এমন একটি সিস্টেম তৈরি করতে পারব যেটা ১ ও ২ চিনতে পারে।
আর দেরি না করে ঝটপট শুরু করলাম,
# Returns the pixel count by category
def pixel_count(digit, index):
# Reading an image, squishing the multidimensional array into single dimension
data = rgb2gray(mpimg.imread(load_digit(digit)[index])).ravel()
ones = [i for i in data if i == 1]
zeros = [i for i in data if i == 0]
value_dict = {
"white_count" : len(ones),
"black_count" : len(zeros)
}
return value_dict
# Comparison between two digits [applying basic statistics]
one_black_pixels = []
one_white_pixels = []
two_black_pixels = []
two_white_pixels = []
for i in range(100):
one_black_pixels.append(pixel_count(1, i)['black_count'])
one_white_pixels.append(pixel_count(1, i)['white_count'])
two_black_pixels.append(pixel_count(2, i)['black_count'])
two_white_pixels.append(pixel_count(2, i)['white_count'])
# Calculating the mean
one_black_pixel_mean = np.mean(one_black_pixels)
one_white_pixel_mean = np.mean(one_white_pixels)
two_black_pixel_mean = np.mean(two_black_pixels)
two_white_pixel_mean = np.mean(two_white_pixels)
print("1 [white] : {0}\n1 [black] : {1}".format(one_white_pixel_mean,
one_black_pixel_mean
))
print(" -- ")
print("2 [white] : {0}\n2 [black] : {1}".format(two_white_pixel_mean,
two_black_pixel_mean
))1 [white] : 646.16
1 [black] : 377.84
--
2 [white] : 726.47
2 [black] : 297.53
অর্থাৎ
**সংখ্যা ১ এর ১০০ টি ইমেজ নিয়ে তাদের সাদা ও কালো পিক্সেলের সংখ্যা গড় করলে আমরা পাই যথাক্রমে $$ 646.16 $$ এবং $$ 377.84 $$ **
সংখ্যা ২ এর ক্ষেত্রে সেটা $$ 726.47 $$ এবং $$ 297.53 $$ এতটি।
একটা পার্থক্য লক্ষণীয়। কিন্তু আমাকে গড় না করে আলাদাভাবে তাদের কাউন্ট দেখতে হবে। গড় সবসময় এক্সট্রিম মানের দিকে ধাবিত হয়।
আমি সংখ্যা ১ ও ২ থেকে প্রতি সংখ্যার ৫০ টি করে স্যাম্পল নেব। তারপর তাদের সাদা পিক্সেল কাউন্টের পার্থক্য একটি অ্যারেতে রাখব। আমি আসলে দেখতে চাচ্ছি ১ ও ২ এর মধ্যে পিক্সেল কাউন্ট কতটা পরিবর্তিত হয়। যদি মিনিমাম পিক্সেল সংখ্যা একদম কম হয় তাহলে আমি তাদেরকে শুধু পিক্সেল কাউন্টের মাধ্যমে আলাদা করতে পারব না।
# Finding out difference between white count between 1 and 2
values = []
for i in range(50):
values.append(abs(pixel_count(1, i)['white_count'] - pixel_count(2, i)['white_count']))
## If checking is needed
#print(values[i])
# Maximum and minimum of the collected difference
print ("Minimum: {0}".format(np.min(values)))
print ("Maximum: {0}".format(np.max(values)))Minimum: 6
Maximum: 335
নাহ, মিনিমাম একদমই কম! যদি ৫০-১০০ হত তাহলে হয়ত একটা থ্রেজহোল্ড দিতে পারতাম, কিন্তু এখন সেটা সম্ভব হবে না। আমি আবার এখানে absolute মান ব্যবহার করেছি। এর মানে হল, এমনও হতে পারে ১ এ সাদা পিক্সেলের সংখ্যা ২ এর চেয়ে বেশি অথবা কম! তার মানে পিক্সেল কাউন্ট পদ্ধতিতে আদৌ বোঝার কোন উপায় নেই!
দিশেহারা হয়ে গেলাম। এমন সময় ফেলুদা ঘরে প্রবেশ করল।
-'সিধুজ্যাঠাকে ফোন করে পেলাম, চল দেখা করে আসি।'
-'ফেলুদা, আমি যে আইডিয়া বের করেছি সেটা কাজ করছে না।'
-'তোর আইডিয়াটা কী ছিল?'
-'সাদা আর কালো পিক্সেল কাউন্ট করে সংখ্যা নির্ধারণ!'
কিছুক্ষণ আঙ্গুল মটকিয়ে ফেলুদা বলল,
-'টোটাল পিক্সেল কাউন্ট যদি প্রায় একই আসে সেক্ষেত্রে তুই পজিশন ভেদে পিক্সেল ডেনসিটি মেজার করতে পারিস। যেমন আমরা ৪ লিখলে মাঝখানের দিকে যতটা কালো পিক্সেল পাওয়া যাবে ০ তে সেই তুলনায় অনেক কম পাওয়া যাবে এবং কোন ক্ষেত্রে যাবেই না।'
-'বুঝলাম না, আরেকটু পরিষ্কার করে বল তো?'
-' $$ 5 \times 5 $$ সাইজের একটা 2D Square Magnifying গ্লাসের কথা চিন্তা কর, এটা আমি ইমেজ ম্যাট্রিক্সের একটা অংশে প্রজেক্ট করলে সেখানকার পিক্সেল গুলো দেখতে পাব, তাই না?'
'হ্যাঁ, তাহলে?'
-'তাহলে ম্যাগনিফাইয়িং গ্লাস টা আমি যদি আরও ডানে ৫ ঘর বা ছবির ক্ষেত্রে পিক্সেল সরাই, তাহলে কী আমি আগের পিক্সেলগুলো দেখতে পাব?'
-'না!', পরক্ষণেই ফেলুদার কথা বুঝতে পারাতে বললাম, 'আচ্ছা তারমানে আমি একটা আর্বিটরারি সাইজের ম্যাট্রিক্স কে এভাবে 2D প্লেনে ইটারেট করে পজিশনওয়াইজ পিক্সেল ডেনসিটি মাপব?!'
-'হ্যাঁ, সেটা পরে করিস, আপাতত আর কথা নয় এক্ষুণি বের হতে হবে আমাদের।'
মনে মনে ফেলুদার তারিফ না করে পারলাম না, ওর অনেকগুলো গুণের মধ্যে একটা হল; নতুন কোন সমস্যা হাতে এলেই ও সেটার উপর স্টাডি করা শুরু করে দেয় এবং যত দ্রুত সম্ভব সেটা সম্পর্কে আপডেটেড হওয়ার চেষ্টা করে। আমি যে কবে শিখব সেটাই বুঝতে পারছি না।
জানুয়ারির মাঝামাঝি, শীত মোটে পড়া শুরু করেছে, তাতেই বাইরে বেশ ঠাণ্ডা, আর বিকেলের দিকে তো এলোমেলো দমকা হাওয়ায় বেরনোই মুস্কিল। সেসব কিছুর তোয়াক্কা না করে একটা পুলওভার চাপিয়ে বের হয়ে গেলাম ফেলুদার সাথে।
-'ফেলু মিত্তির, এতদিন পর হঠাৎ স্মরণ করলে যে? পসার খুব বেড়ে গেছে মনে হয়?', সোফায় বসে বললেন সিধুজ্যাঠা।
-'আপনার আশীর্বাদে তা কিছুটা বেড়েছে বৈকি!'
-'তুমি নিশ্চয়ই অধ্যাপক হত্যাকাণ্ডের ব্যাপারে আমার সাথে দেখা করতে এসেছ?'
একটা চওড়া হাসি দিয়ে ফেলুদা বলল, 'কীভাবে বুঝলেন?'
-'কারণ, তুমি জান আমি ইন্টারেস্টিং ঘটনা পড়তে ও সংগ্রহ করতে ভালবাসি, শুধু শুধু একজন মধ্যবিত্ত অধ্যাপককে কেন খুন করা হল সেটা বেশ রহস্যজনক ব্যাপার। ভদ্রলোক যেহেতু ওপেনসোর্স অ্যাক্টিভিটির সাথে জড়িত ছিল, তোমার ধারণা সেকারণেই হয়ত উনি খুন হন। আর আমি নিজেও ওপেনসোর্স কমিউনিটির একজন অ্যাক্টিভ সদস্য ছিলাম। তাই দুইয়ে দুইয়ে চার করতে কোন সমস্যা হয় নি।'
-'আপনি গোয়েন্দাগিরি করলে আমাদের মত প্রাইভেট ইনভেস্টিগেটরদের পথে বসতে হত!', পরিবেশ হাল্কা করে ফেলুদা বলল।
-'হাহা, আমি অনেক কিছু করলে অনেকেরই পথে বসতে হত, তাই কিছুই করিনি! শুধু মাইন্ড ওপেন রেখে যতটা সম্ভব জ্ঞানার্জন করা যায় শুধু সেই পথেই হাঁটছি! তা বল, কী জানতে চাও?'
-'অধ্যাপকের পাশাপাশি শশাঙ্ক মুখার্জী নামের একজন ভদ্রলোক খুন হন, ওনার পেশা জানা যায় নি। এমনকি প্রতিবেশীরাও জানে না এ ব্যাপারে কিছু বলতে পারছে না। আমি ধারণা করছি এই দুই ভদ্রলোকই কোনভাবে সম্পর্কিত। অভিয়াসলি এটাও একটা কারণ যে তাঁদেরকে একইভাবে হত্যা করা হয়। আপনি শশাঙ্কবাবু সম্পর্কে কিছু জানেন কিনা সেটা জিজ্ঞাসা করতে আসলাম'
কিছুক্ষণ সবাই চুপচাপ, বেয়ারা এসে চা, চানাচুর আর বিস্কুট দিয়ে গেল। কিছু করার ছিল না দেখে আমি একটা বিস্কুট নিয়ে খেতে শুরু করলাম। সিধুজ্যাঠা বললেন, 'নাহ, নামটা একদম মনে পড়ছে না, আচ্ছা এক মিনিট।', বলেই ঘরের ভেতরে চলে গেলেন।
ঠিক প্রায় তৎক্ষণাৎই একটা বই হাতে প্রবেশ করলেন,
'এটাকে বলতে পারো ওপেনসোর্স কন্ট্রিবিউটর ডিরেক্টরি, এখন এইসব জিনিস আমার কাছে আছে জানলে পুলিশে ধরে নিয়ে যাবে। যদি শশাঙ্কবাবু সত্যিই ওপেনসোর্স অ্যাক্টিভিটির সাথে জড়িত থাকেন তাহলে অবশ্যই তার বায়ো এখানে থাকবে।'
বলে বইটা টেবিলে রেখে পাতা ওল্টাতে শুরু করলেন। আমি বেশ আগ্রহের সাথে দেখতে থাকলাম। টেকনোলজিক্যাল অ্যাডভান্সমেন্টের অন্যতম হাতিয়ার ওপেনসোর্স কন্ট্রিবিউশন। এত এত কোম্পানি দাঁড়িয়ে আছে ওপেনসোর্স টুলস কে পুঁজি করে। হয়ত কন্ট্রিবিউশন এখন নিষিদ্ধ কিন্তু রিসার্চ থেকে শুরু করে সবকাজের ভিত্তি ছিল এই ওপেন সফটওয়্যার স্ট্যাক।
ডিরেক্টরি ঘাঁটতে ঘাঁটতে সিধুজ্যাঠা বললেন, 'নাহ এখানে তো ওই নামে কাউকে খুঁজে পাচ্ছি না!' এমন সময় আমি জোরে বলে উঠলাম, 'সিধু জ্যাঠা থামুন!'
সিধুজ্যাঠা চমকে আমার দিকে তাকাতে ফেলুদা ডিরেক্টরি থেকে চোখ না সরিয়ে বলল, 'মানসবাবুও তাহলে ওপেনসোর্স কন্ট্রিবিউটর ছিলেন!'
-'ও আচ্ছা উনি? উনি তো তেমন কন্ট্রিবিউট করতেন না, তখন একটা ট্রেন্ড ছিল এবং কন্ট্রিবিউটরদের অন্য চোখে দেখা হত। উনি বোধহয় হুজুগে নিজে নাম এন্ট্রি করেছিলেন। উল্লেখযোগ্য কোন কন্ট্রিবিউশন তার ঝুলিতে নেই। তোমরা চেনো কীভাবে এঁকে?' বললেন সিধু জ্যাঠা।
-'সে অনেক কাহিনী সিধু জ্যাঠা, আপনাকে অন্য সময় বলব। হতে পারে এটা কোইন্সিডেন্স, শশাঙ্ক মুখার্জীর মৃত্যুর কারণ হয়ত অন্য কিছু। যাই হোক, একটা সিস্টেম বিল্ড করতে চাচ্ছি সেটা হাতে লেখা বাংলা ডিজিট রিকগনাইজ করতে পারে। তোপসেই মূল কাজ করছে কিন্তু এ ব্যাপারে আপনার মতামত শুনলে ভাল হত!', বলল ফেলুদা।
-'আচ্ছা, তোমরা নিশ্চয়ই নলেজ বেজড মেথডে আগাচ্ছ? সেটা খুব একটা ভাল কাজ করবে না, তোমরা বরং স্ট্যাটিসটিক্যাল ও প্রব্যাবিলিস্টিক অ্যানালাইসিস কর। আমি একটা বই দিয়ে দিচ্ছি, পড়লে বেশ কিছু জিনিস পরিষ্কার হবে। আর কোন কিছু ইম্প্লিমেন্টেশনে সমস্যা হলে আমাকে বলতে পার। তবে ঘুণাক্ষরেও কেউ যেন টের না পায় তোমরা এ জিনিস ডেভেলপ করছ!'
বলে সিধুজ্যাঠা আবারও ঘরে চলে গেলেন ও কিছুক্ষণ পরেই চলে আসলেন, তার হাতে একটা ছোট বই। বইটা ফেলুদার হাতে দিয়ে বললেন, 'বইটা বেশ ভাল, তবে আবারও একই কথা। খুব সাবধানে কাজ করবে। বেস্ট অফ লাক!'
প্রব্যাবিলিটি কলেজে থাকতে পড়েছিলাম, মনে নেই কি পড়েছিলাম। সম্ভবত বুঝিনি, যাই হোক সিধু জ্যাঠার দেওয়া বইটার নাম, A First Course in Probability।
বাড়িতে ফিরেই আমাকে ফেলুদা বলল, 'আমি রাতে আর কিছু খাব না, ডিস্টার্ব করবি না একদম। যে কাজ দিয়েছি গুডবয়ের মত করে রাখিস, তোর সাথে এ নিয়ে কাল আমার কথা হবে। বুঝেছিস?'
আমি মাথা নেড়ে নিজের ঘরে চলে গেলাম। কাজটা করতে বেশ আলসেমি লাগছিল। তাই মনস্থির করলাম একটু বাইরে থেকে বেড়িয়ে আসি।
রাতের বেলা ফিরে শংকরকে ফেলুদার কথা জিজ্ঞেস করতে বলল, 'ফেলুবাবু তো ঘর থেকে বের হননি, তোমার খাবার কি দিয়ে দেব?'
আমি মাথা নেড়ে চিন্তা করতে থাকলাম, ফেলুদা কি আজকের মধ্যে বইটা শেষ করবে নাকি? নাকি ও রহস্যের জট ছাড়াচ্ছে? আর বেশিক্ষণ চিন্তা করলে হয়ত আমার নিজের মাথায়ই জট লেগে যেত তাই আমি চিন্তা করা বাদ দিয়ে খেয়ে ঘুমিয়ে গেলাম।
সকালে উঠেই বৈঠকখানায় ফেলুদাকে পেয়ে গেলে বললাম, 'কিছু কূলকিনারা করতে পারলে?'
ফেলুদা সে কথার জবাব না দিয়ে হাতের কয়েন দেখিয়ে বলল, ''এই কয়েনটা আমি যদি টস করি তাহলে $$ Head $$ উঠবে নাকি $$ Tail $$ ?
বললাম, 'এত খুব সহজ, ৫০%-৫০% চান্স!'
-'তুই ৫০-৫০ কীভাবে হিসাব করলি? আর এক্স্যাক্টলি বলতে পারবি হেড হবে নাকি টেইল?'
-'ইনটুইশন দিয়ে! এক্স্যাক্টলি কি হবে সেটা বলতে পারব না, সেতো খুব কঠিন কাজ!'
আচ্ছা, এবার আরেকটা প্রশ্ন করি,
-'ধর, আমি কয়েনটা একটু বাঁকিয়ে ফেললাম। এরপর তোকে বললাম, পরপর তিন টসে দুইটা হেড ওঠার সম্ভাবনা কত?'
কিছুক্ষণ মাথা চুলকে বললাম, 'নাহ ফেলুদা, পারছি না!'
-"পড়ালেখা কি করিস কিছু? কি ম্যাথ শিখায় তোদের স্কুলে? তোকে ধমক দিয়ে আসলে লাভ নেই, শিক্ষাব্যবস্থাই এরকম। গণিতে আমরা ইনটুইশন থেকে কম্পিউটেশন বেশি করি আর সে কারণেই ম্যাথ বোরিং লাগে। কম্পিউটেশনের জন্য আমাদের তো কম্পিউটার আছেই। সবথেকে বেশি জরুরি ইনটুইশন।"
"আচ্ছা এটা বলতে পারবি কেন এক্স্যাক্টলি বলাটা টাফ যে $$ n^{th} $$ টস $$ Head $$ হবে নাকি $$ Tail $$ ?"
মাথা নাড়তেই ফেলুদা বলল, "নাহ, তোকে দিয়ে কিচ্ছু হবে না। এখন দেখ, " ধমক দিয়ে ফেলুদা একটা কাগজে লেখা শুরু করল সাথে বলতে লাগল,
"ধর এটা একটা কয়েন যেটা আমি টস করব, ফিজিক্সে একে যদি আমি ইক্যুয়েশন দিয়ে মডেল করতে চাই তাহলে ব্যাপারটা হবে এরকম"
"দেখেছিস কতটা জটিল হয়ে যাচ্ছে? এসব প্রবলেমকে ম্যাথেমেটিক্যালি হ্যান্ডেল করতে ও জটিল মডেল সিম্পল করতে আমরা প্রব্যাবিলিটির সাহায্য নেই। আমি যদিওবা কোনভাবে ফিজিক্স খাটিয়ে মডেল তৈরি করি তবুও তুই অতগুলো মান কখনোই ওই সময়ে মাপতে পারবি না। আচ্ছা তুই যে ৫০-৫০% চান্স বললি, সেটা কী হাতে কলমে দেখাতে পারবি?"
নাহ, সেটাও আমার দ্বারা সম্ভব না, তাই চুপ করে থাকাই বুদ্ধিমানের কাজ মনে হল।
ফেলুদা ওর ল্যাপটপ বের করে পাইথনে একটা কোড লিখল,
import numpy as np
import matplotlib.pyplot as plt
# Expressing Head|Tail in terms of 1|0
TAIL = 0
HEAD = 1
SMALL_SAMPLE_COUNT = 10
LARGE_SAMPLE_COUNT = 5000
## Taking 10 samples & 5000 samples for plotting histogram
coin_toss_10_samples = np.random.choice([TAIL, HEAD], SMALL_SAMPLE_COUNT)
coin_toss_5000_samples = np.random.choice([TAIL, HEAD], LARGE_SAMPLE_COUNT)
data = [coin_toss_10_samples, coin_toss_5000_samples]
titles = ['10 Coin Toss Result', '5000 Coin Toss result']
f, a = plt.subplots(2, 1)
a = a.ravel()
for index, axis in enumerate(a):
axis.hist(data[index])
axis.set_title(titles[index])
axis.set_xlabel("Heads or Tails")
axis.set_ylabel("Head / Tail Count")
plt.tight_layout()
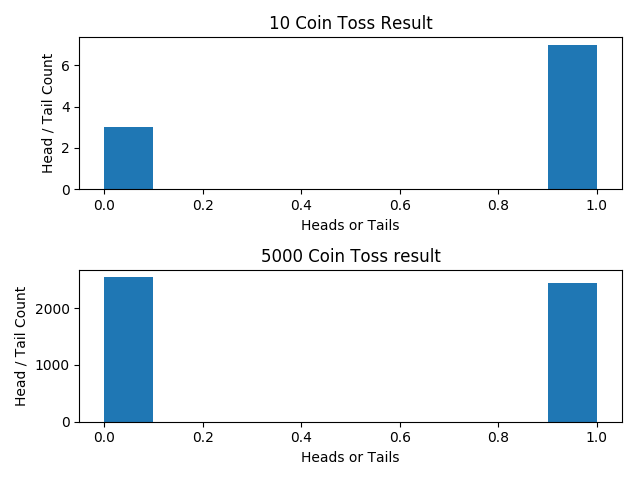
plt.show()রান করাতে এটা আসল,
"প্রথমে আমি যখন ১০ বার টস করলাম, দেখ যতটা না $$ Tail $$ এসেছে তার তুলনায় $$ Head $$ এর সংখ্যা বেশি (দ্বিগুণেরও বেশি!)। কিন্তু আমি যখন ৫০০০ বার টস করলাম তখন দেখ পার্থক্য কতটা কমে আসছে? এখন কিন্তু বলা যেতেই পারে $$ Head:Tail = 50:50 (approx) $$ । $$ Central \space Limit \space Theorem $$ বলে, স্যাম্পলের সংখ্যা যত বেশি হবে.."