logreg_distribution.md

লজিস্টিক রিগ্রেশন : প্রব্যাবিলিটি, বার্নুলি ও বাইনোমিয়াল ডিস্ট্রিবিউশন

গত অধ্যায়ে আমরা দেখেছিলাম, ক্লাসিফিকেশন প্রবলেমগুলো লিনিয়ার রিগ্রেশন দিয়ে করলে কী কী সমস্যা হতে পারে। পাশাপাশি আলোচনা করা হয়েছিল ডিসিশন বাউন্ডারি, লগিট বা সিগময়েড ফাংশন নিয়ে।

এই ব্যাপারে সবার একমত হওয়া উচিৎ যে, ক্লাসিফিকেশন সমস্যা সল্ভ করতে হলে একটু ভিন্ন উপায়ে আগাতে হবে। কারণ, আমরা যে লস ফাংশন নিয়ে কাজ করছি, সেটা মিসক্লাসিফিকেশন মাপার জন্য ভাল না।

প্রশ্ন হচ্ছে আমরা তাহলে ক্লাসিফিকেশন এরর টা মেজার করব কীভাবে? সেটা নিয়েই আজকের অধ্যায়।

আজকের টপিক:

• প্রব্যাবিলিট ও কন্ডিশনাল প্রব্যাবিলিটি

• ইনডিপেন্ডেন্স

• প্রব্যাবিলিটির সাম ও প্রোডাক্ট রুল

• Bernoulli ট্রায়াল

• Bernoulli ডিস্ট্রিবিউশন

• Binomial ডিস্ট্রিবিউশন

---

প্রব্যাবিলিটি

ফরমাল ইক্যুয়েশন নিয়ে কথা না বলে বরং একটা উদাহরণ দিয়ে ব্যাখ্যা করা যাক। আমি এখানে গ্রাফিক্যাল মডেল দিয়ে ব্যাখ্যা করার চেষ্টা করব।

খুনের রহস্য

ধরি একটা বাড়িতে বাড়ির মালিক খুন হল। আমাদের প্রব্যাবিলিস্টিক অ্যাপ্রক্সিমেশন দিয়ে বের করতে হবে সেটা কে করেছে।

আরও ধরা যাক সাসপেক্ট দুইজন

• বাড়ির চাকর
• বাড়ির রাঁধুনী

এবং অস্ত্র তিনটা

• চাকু
• পিস্তল
• সূক্ষ্ম ও ধারালো লোহার রড

প্রায়োর ডিস্ট্রিবিউশন (Prior Distribution)

Prior বা প্রায়োর হল, অ্যাপ্রক্সিমেশন করার আগে বেসিক কিছু ধারণা নিয়ে কাজ শুরু করতে হয় যেটাকেই প্রায়োর বলে।

এই সমস্যার প্রায়োর হল এটা,

• বাড়ির চাকর এই পরিবারে অনেকদিন ধরে আছে এবং বিশ্বাসভাজন
• আর রাঁধুনীকে বেশিদিন হল নিয়োগ দেয়া হয় নি, এবং তার সম্পর্কে কিছু গুজবও আছে

এই প্রায়োর জ্ঞান দিয়ে আমরা ধারণা করে ফেলতে পারি, রাঁধুনীই আসল খুনি! এবং চাকরের খুনি হওয়ার সম্ভাবনা অনেক কম। ম্যাথেমেটিক্যাল নোটেশনে লিখতে চাইলে এভাবে লিখব, $$ \begin{align} P(Culprit=Servant) = 20% \ P(Culprit=Cook) = 80% \end{align} $$ এখানে Culprit একটা ভ্যারিয়েবল যার স্টেট দুইটা হতে পারে, একটি হল Servant এবং আরেকটি হল Cook। যেহেতু আমরা এখন পর্যন্ত রহস্য সমাধান করতে পারি নি তাই Culprit এর আসল স্টেট আমাদের কাছে অজানা।

প্রব্যাবিলিটির সাম রুল (Sum Rule of Probability)

কিন্তু, $$ P(Culprit=Servant) + P(Culprit=Cook) = 100% $$ তারমানে একটা ব্যাপারে আমরা নিশ্চিৎ, খুনি Servant অথবা Cook এদের মধ্যে কেউ একজন। এটা হল Sum Rule of Probability।

উপরের সমীকরণ দুইটা দিয়ে আসলে প্রব্যাবিলিটি ডিস্ট্রিবিউশন বুঝানো হচ্ছে।

এখানে অনেক প্রশ্ন আসতে পারে, আশি পার্সেন্ট কেন? $$83%$$ হলে কি সমস্যা? উত্তর হল এটা আমাদের একটা ধারণা, আসল পার্সেন্ট কত সেটা আমরা প্রাপ্ত ডেটা থেকে Infer বা প্রেডিক্ট করব। আমরা ডেটা নিয়ে কাজ শুরুই করিনি।

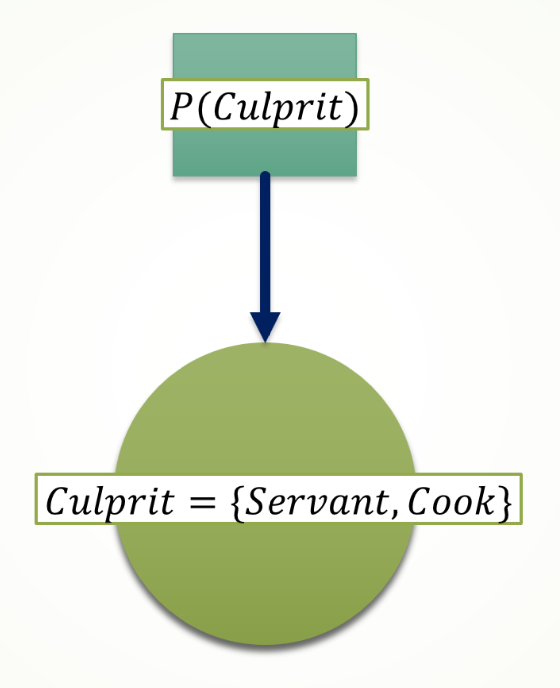
গ্রাফিকাল নোটেশন প্রব্যাবিলিটির ডিপেন্ডেন্সি ও ইন্ডিপেন্ডেন্সি ভালভাবে দেখাতে পারে। তাই এই নোটেশনগুলোকে গ্রাফিক্যালি রিপ্রেজেন্ট করার চেষ্টা করব। নিচের ছবিটা হল একটা Factor Graph। যেটা সম্পর্কে পরেই বিস্তারিত বলা হবে।

Node: এটা দ্বারা র‍্যান্ডম ভ্যারিয়েবল বুঝায়, এখানে যেটা হল Culprit এবং যার দুইটা স্টেট হল Servant, Cook। অথবা, $$Culprit = {Servant, Cook }$$

Square: বর্গ দিয়ে প্রব্যাবিলিটি ডিস্ট্রিবিউশন বুঝায়। অর্থাৎ, $$P(Culprit)$$।

কন্ডিশনাল ডিস্ট্রিবিউশন (Conditional Distribution)

ধরি,

• বাড়ির চাকরের লাইসেন্সড পিস্তল ব্যবহার করার অভিজ্ঞতা আছে। এবং সে পার্সোনাল ড্রয়ারে পিস্তল লকড অবস্থায় রাখে। কিন্তু চাকরের বয়স অনেক বেশি।
• রাঁধুনীর স্বাভাবিকভাবেই চাকুর অ্যাক্সেস আছে।

এখানে কালপ্রিট স্টেট দুইটা, তাই প্রতি স্টেটে আমরা অস্ত্রের একটা প্রব্যাবিলিটি টেবিল তৈরি করি তাহলে নিচের মত দেখা যাবে।

খুনি 'যদি' রাঁধুনী হয়, তাহলে সে কোন অস্ত্র ব্যবহার করবে?

Pistol	Knife	Rod
5%	65%	30%

স্বাভাবিকভাবেই রাঁধুনী চাকু দিয়ে খুন করার চেষ্টা করবে যেহেতু তার কাছে সেই অস্ত্রের অ্যাকসেস পাওয়া সবেচেয়ে সহজ। এখানে সব প্রব্যাবিলিটির মান যোগ করলে ১০০% হচ্ছে। কারণ, যদি খুনি আসলেই রাঁধুনী হয়ে থাকে, তাহলে ওই তিনধরণের যেকোন একটি দিয়ে সে খুন করেছে। আর যেহেতু ওই তিনটা ছাড়া কোন অপশন নাই তাই তিনটার যেকোন একটা হওয়ার প্রব্যাবিলিটি শতভাগ।

খুনি 'যদি' চাকর হয়, তাহলে

Pistol	Knife	Rod
80%	10%	10%

এটাও কনভিনসিং লাগছে, তাই না?

এটা কিন্তু ডেটার ভিত্তিতে আমরা Assume করে নিচ্ছি।

এখন যদি ম্যাথমেটিক্যালি লিখতে যাই, $$ \begin{align} P( Pistol| Servant) = 80%\ P(Knife | Servant) = 10% \ P(Rod | Servant) = 10 % \end{align} $$ সাধারণভাবে আমরা বলি, Probability of Weapon (Example: Knife) given the Culprit (Example: Servant).
$$ P(Weapon | Culprit) $$ এখানে Weapon আরেকটি র‍্যান্ডম ভ‍্যারিয়েবল যার স্টেট তিনটা, Pistol, Knife, Rod।

যখনই আমরা কোন একটা ঘটনাকে বাছাই করি, সেটা হয়েছে কিনা, আমরা আসলে তার ডিপেন্ডেন্ট স্টেট গুলোকে জুম করে দেখি। নিচের ছবি দিয়ে পরিষ্কার বোঝা যাবে। [The figure will be added later]

তারমানে Culprit র‍্যান্ডম ভ্যারিয়েবল ইনডিপেন্ডেন্ট, কিন্তু ‍Weapon এর স্টেট কোনটা হবে সেটা Culprit এর উপর ডিপেন্ডেন্ট।

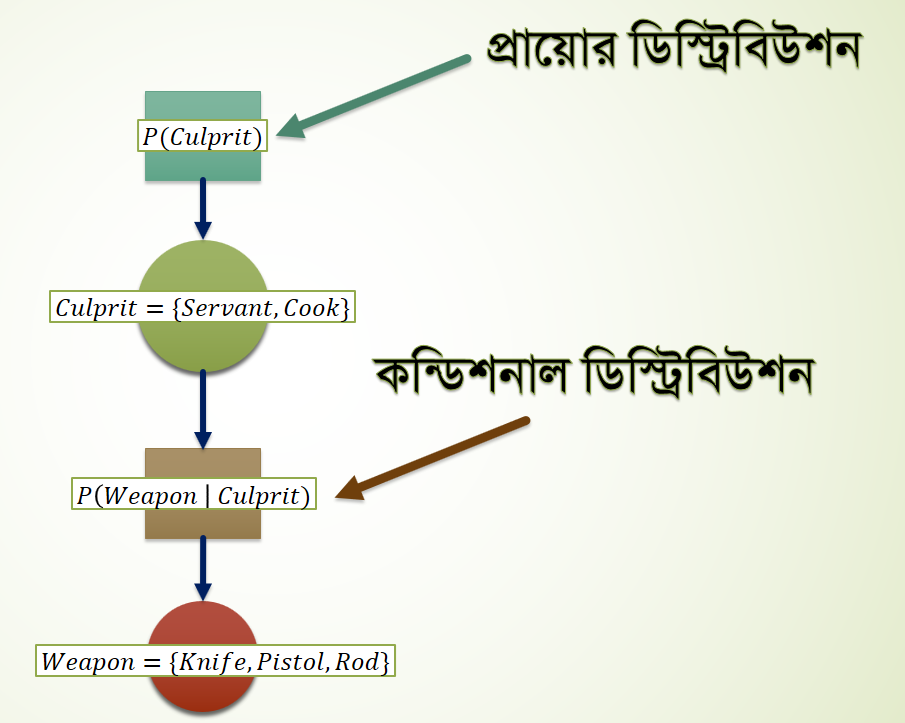
পরিবর্তিত Factor Graph,

অ্যারো চিহ্ন দিয়ে কোনটা কার উপর নির্ভরশীল বা কন্ডিশনাল ডিপেন্ডেন্ট সেটা বুঝানো হচ্ছে।

জয়েন্ট ডিস্ট্রিবিউশন (Joint Distribution)

জয়েন্ট ডিস্ট্রিবিউশন হল যতগুলো র‍্যান্ডম ভ্যারিয়েবল আছে তাদের জয়েন্টলি যে ডিস্ট্রিবিউশন সেটা। যেমন এখানে Culprit আর Weapon এর সম্মিলিত প্রব্যাবিলিটি ডিস্ট্রিবিউশন ই হবে তাদের জয়েন্ট ডিস্ট্রিবিউশন।

নিচের প্রশ্নের উত্তর আমরা জয়েন্ট ডিস্ট্রিবিউশন দিয়ে দিতে পারব,

রাঁধুনীর পিস্তল দিয়ে হত্যা করার সম্ভাবনা কত?

এই প্রশ্নের মধ্যে আসলে দুইটা প্রশ্ন আছে। প্রথমটি হল, "খুনির রাঁধুনী হওয়ার সম্ভাবনা কত? (যদি খুনি রাঁধুনী হয়)" দ্বিতীয়টি হল, "খুনির পিস্তল দিয়ে হত্যা করার সম্ভাবনা কত?"।

• প্রথম প্রশ্নের উত্তর $$P(Culprit=Cook) = 80 %$$
• দ্বিতীয় প্রশ্নের উত্তর $$P(Weapon = Pistol | Culprit = Cook) = 5 % $$

তাহলে রাঁধুনীর পিস্তল দিয়ে হত্যা করার সম্ভাবনা হচ্ছে, $$ \begin{align} P(Pistol, Cook) &= P(Pistol \cap Cook) \ &= P(Pistol | Cook) \times P(Cook) \ &= 5% \times 80% \ &= 4%
\end{align} $$ একে Product Rule of Probability বলা হয়ে থাকে। জেনারেল ফর্মে লেখে এভাবে, $$ P(x, y) = P(y | x) P(x) $$ এভাবে আমরা আরও পাঁচটি কম্বিনেশন তৈরি করতে পারি। যেমন, রাঁধুনীর চাকু/রড দিয়ে হত্যা করার সম্ভবনা কত বা চাকরের পিস্তল/চাকু/রড দিয়ে হত্যা করার সম্ভাবনা কত। এই মোট ছয়টি কম্বিনেশনের একটি টেবিল নিচে ক্যালকুলেট করে দেয়া হল

-	Pistol	Knife	Rod
Cook	4%	52%	24%
Servant	16%	2%	2%

Likelihood এবং Probability এর মধ্যে সূক্ষ্ম তফাৎ আছে যেটা পরে বলা হবে।

মার্জিনাল ডিস্ট্রিবিউশন (Marginal Distribution)

জয়েন্ট ডিস্ট্রিবিউশন থেকে আমরা সহজেই মার্জিনাল ডিস্ট্রিবিউশন বের করতে পারি। মার্জিনাল ডিস্ট্রিবিউশন মানে হল র‍্যান্ডম ভ্যারিয়েবলের কোন একটা স্টেট সিলেক্ট করে, সে স্টেটের যতগুলা প্রব্যাবিলিটির মান জয়েন্ট ডিস্ট্রিবিউশনে আছে তার যোগ করা।

না বুঝা গেলে, আমরা যদি Pistol এর মার্জিনাল ডিস্ট্রিবিউশন বের করতে চাই তাহলে, $$ \begin{align} P(Pistol) &= P(Pistol | Cook) + P(Pistol | Servant) \ &= 4% + 16% \ &= 20% \end{align} $$ Cook এর মার্জিনাল ডিস্ট্রিবিউশন বের করব এভাবে, $$ \begin{align} P(Cook) &= P(Cook | Pistol) + P(Cook | Knife) + P(Cook | Rod) \ &= 4% + 52% + 24% \ &= 80% \end{align} $$ অর্থাৎ আমরা যেটা Prior ধরেছিলাম সেটাই। বাকি মার্জিনাল ডিস্ট্রিবিউশনও এভাবে বের করতে পারেন।

জেনারেল সূত্র হল, $$ P_{X}(x)= \sum_{y}P_{X, Y}(x, y) $$ $$ P_{X, Y}$$ কে আবার কন্ডিশনাল ফর্মে লেখা যায়, $$ P_{X}(x) = \sum_{y}P_{Y}(y)P_{X|Y}(x|y) $$ এটা গেল ডিস্ক্রিট ডেটার ক্ষেত্রে, কন্টিনিউয়াস ডেটার ক্ষেত্রে সামেশনের জায়গায় ইন্টিগ্রেশন বসবে।

ইন্ডিপেন্ডেন্স

ভ্যারিয়েবলের উপর যদি অন্য কোন ভ্যারিয়েবল দ্বারা শর্ত আরোপ করলেও সেটার উপরে ওই ভ্যারিয়েবলের কোন স্টেট হওয়ার সম্ভাবনা অপরিবর্তিত থাকে তাহলে যে ভ্যারিয়েবলের উপর শর্ত আরোপ করা হয়েছিল সেটা ইন্ডিপেন্ডেন্ট বা স্বাধীন ভ্যারিয়েবল।

যদি বলা হয়, পর পর দুইটা কয়েন টসে Head উঠার সম্ভাবনা কত? যদি বাইরে বৃষ্টি পড়ে? [ধরি কয়েনটা Fair] $$ \begin{align} P(Result = Head, Head| Weather = Rainy) &= P(Head | Rainy) \times P(Head|Rainy) \ &= P(Head) \times P(Head) \ &= 50% \times 50% \ &= 25% \end{align} $$ বাইরে বৃষ্টি পড়ুক বা না পড়ুক, তাতে টসে হেড উঠবে না টেইল উঠবে তা ডিপেন্ড করে না। তাই আমরা ওটা এড়াতে পারি।

এই বিষয়টা খুব সাধারণ মনে হলেও এটা মারাত্মক শক্তিশালী একটি কনসেপ্ট, পরবর্তী টপিকগুলোতে বারংবার এটা আসবে (Example: Naive Bayes)।

বার্নুলি ট্রায়াল (Bernoulli Trial)

বার্নুলি ট্রায়াল হল, কোন একটা ঘটনার ফলাফল যদি শুধু হ্যাঁ/না; 1/0; স্টেট-১/স্টেট-২; সাক্সেস/ফেইলিওর এর মধ্যে সীমাবদ্ধ থাকে তাহলে আমরা তাকে Bernoulli Trial বলব।

উদাহরণ: যেমন কয়েন টস, বৃষ্টি হবে কি না, হ্যাঁ/না ভিত্তিক প্রশ্নের উত্তর ইত্যাদি।

বার্নুলি ডিস্ট্রিবিউশন (Bernoulli Distribution)

ধরি, Head ওঠার সম্ভাবনা যদি 0.5 হয় তাহলে Tail উঠার সম্ভাবনা কত? অবশ্যই 0.5। আবার Head ওঠার সম্ভাবনা যদি 0.7 হয় তাহলে? Tail ওঠার সম্ভাবনা? 0.3! একে ম্যাথেমেটিক্যালি প্রকাশ করা হয় এভাবে, $$ P(Head|0.5)=0.5^{Head} \times (1-0.5)^{Tail } $$ Head কে যদি 1 বলি আর Tail কে 0, সেক্ষেত্রে Head ওঠার সম্ভাবনা, $$ P(1 | 0.5)=0.5^{1} = 0.5 $$ এবং Tail ওঠার সম্ভাবনা, $$ P(0|0.5) = 0.5^{0} \times (1-0.5)^{1-0} = 0.5 $$ গাণিতিকভাবে প্যাক করলে, $$x \in {1, 0}$$ এবং $$\theta =[0, 1]$$
$$ Bern(x|\theta) = \theta^{x}(1-\theta)^{1-x} $$ এটাই হল বার্নুলি ডিস্ট্রিবিউশন! [মনে রাখতে হবে আমি টস করেছি কিন্তু মাত্র একবার!]

বাইনোমিয়াল ডিস্ট্রিবিউশন (Binomial Distribution)

এখন আপনাকে যদি বলা হয়, একটা Fair কয়েন আপনি 10 বার টস করবেন এখন এতে Head ৫ বার ওঠার সম্ভাবনা কত? (যদি প্রতি টসের আগের টসের ফলাফল Tail)। 5 টা Head উঠলে বাকি 5 টা অবশ্যই Tail। যেহেতু আমি ১০টা টস বিবেচনা করছি তাই আমার Tail ও গণনায় ধরতে হবে।

তাহলে আমি সমস্যা এভাবে মডেল করতে পারি, $$ \begin{align} P(Head , Count =5 | Previous , Result = Tail)
&= P(T) \times P(H|T) \times P(T) \times P(H|T) \times P(T) \times P(H|T) \times P(T) \times P(H|T) \ &= P(H|T)^5 \times P(T)^5 \ &= P(H)^5 \times P(T)^5\ &= 0.5^5 \times 0.5^5 \times 100 \ &= 0.09% \end{align} $$ প্রশ্ন আসছে, আমি $$P(H|T)$$ থেকে কীভাবে $$P(H)$$ এ গেলাম? আচ্ছা আপনিই চিন্তা করে দেখুন, পরের টসের রেজাল্ট কী হবে সেটা কি আগের টসের রেজাল্টের উপর নির্ভরশীল? অবশ্যই নয়! তাই আমি এই শর্ত সম্পূর্ণ উপেক্ষা করে সাধারণভাবে Head - Tail ওঠার প্রব্যাবিলিটি দিয়ে গুণ দিতে পারি। এটাই ইন্ডিপেন্ডেন্স।

কিন্তু একে ম্যাথেমেটিক্যালি কীভাবে লিখতে পারা যায়? ধরি টস সংখ্যা $$N=10$$ এবং রেজাল্ট Head হতে হবে 5 বার তাই $$m=5$$ এবং টসে Head হওয়ার সম্ভাবনা $$\theta=0.5$$ সুতরাং, ৫ বার Head হওয়ার সম্ভাবনা $$ P(m=5 | N=10, \theta=0.5) = 1 \times 0.5^{5} \times (1-0.5)^{10-5} $$ জেনারেল ফর্মে, $$ Bin(m |N, \theta) = \binom Nm \theta^{m}(1-\theta)^{N-m} $$ কিন্তু প্রশ্ন থেকেই যাচ্ছে, $$\binom Nm$$ আসল কোথা থেকে? এটা দিয়ে বুঝাচ্ছি $$N$$ টসে $$m$$ সংখ্যক আউটকাম কতভাবে বাছাই করা যায় (Permutation & Combination)। $$\binom {10}5$$ এর মান যেহেতু $$1$$ তাই সেটা দিয়ে গুণ করা হয়েছে আর সবকিছু সিম্পল রাখার জন্য প্রথমে আমি উহ্য রেখেছি। Maximum Likelihood Estimation এ আমরা এই কম্বিনেশন নিয়ে কাজ না করলেও সমস্যা নেই। কেন নেই তা পরবর্তী অধ্যায়ের জন্য তোলা থাকল।

বাইনোমিয়াল ডিস্ট্রিবিউশন প্লট

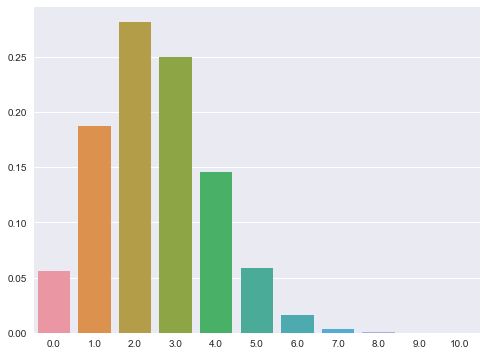
এখন একটু কোড চলে যাওয়া যাক, যদি $$N=10$$ এবং $$\theta=0.25$$ হয়। তারমানে টসে Head ওঠার সম্ভাবনা 25%, অন্য কথায় কয়েনটা হাইলি বায়াসড। তাহলে তার ডিস্ট্রিবিউশন প্লট কিরকম হবে?

import seaborn as sns
import matplotlib.pyplot as plt
import scipy

plt.figure(figsize=(8, 6))

theta = 0.25
N = 10

head_counts = scipy.linspace(0,10,11) # Number of head counts

pmf = scipy.stats.binom.pmf(head_counts,N,theta)
sns.barplot(head_counts, pmf)

আউটপুট

এখানে $$X$$ এক্সিসে দেখানো হচ্ছে $$m$$ এর বিভিন্ন মান আর $$Y$$ এক্সিসে দেখানো হচ্ছে সেটা হওয়ার সম্ভাবনা কতটুকু। যেহেতু আমরা এখানে বলেছি, $$\theta$$ এর মান $$0.25$$ তাই $$m=2$$ ও এর আশেপাশের বার গুলো আকারে লম্বা, মানে ১০ টি টসে $$\theta=0.25$$ হলে ২ টি হেড ওঠার সম্ভাবনা বেশি। এভাবে $$N$$ , $$m$$ ও $$\theta$$ পরিবর্তন করে আমরা বের করতে পারি কতগুলা টসে কত হেড উঠবে।

পরবর্তী অধ্যায়ে ম্যাক্সিমাম লাইকলিহুড এস্টিমেশন নিয়ে আলোচনা করা হবে।