diff --git a/readme.md b/readme.md index a8ebbac..91164e0 100644 --- a/readme.md +++ b/readme.md @@ -149,7 +149,7 @@ $$ #### RNN Cell -​ 每一个 RNN 神经元接受 160 个比特的串作为输入，这里将其记为 $I_i = J_{i1}J_{i2}J_{i3}J_{i4}J_{i5}$，其中 $J_{ij}$ 是一个 32 比特的串。我们令 $Q_1 \sim CS, Q_2 \sim CS$，然后令 $W_i \sim CS , 1\le i\le5$，定义 32 位乘法为将乘法结果的高 32 位与低 32 位异或： +​ 每一个 RNN 神经元接受 160 个比特的串作为输入，这里将其记为 $I_i = J_{i1}J_{i2}J_{i3}J_{i4}J_{i5}$，其中 $J_{ij}$ 是一个 32 比特的串。我们令 $Q_1 \sim CS, Q_2 \sim CS$，然后令 $W_i \sim CS , 1\le i\le5$，定义 32 位乘法为将乘法结果的高 32 位与低 32 位进行或运算： $$ F_1 \leftarrow J_{i1} \times W_1 + J_{i2} \times W_2 + J_{i3} \times W_3 + prev \\ F_2 \leftarrow J_{i4} \times W_4 + J_{i5} \times W_5 @@ -186,7 +186,7 @@ H_{7}=D_{2} \oplus D_{3} \oplus t_{1} \\ \text { where } t_{1}=C h\left(D_{1}, D_{2}, D_{3}\right) \oplus D_{4} \oplus \Sigma 1\left(D_{3}\right) \end{array}\right. $$ -​ 非线性激活层首先定义 $h_i = J_i\oplus J_{i+5}, 1\le i \le5$，其中 $J_i = W_i \times I_i$，$W_i \sim CS$，$I_i$ 是将输入的 320 比特等分成 10 份中的结果，长度为 32 比特，这里 $1 \le i \le 10$。32 位乘法定义为两数相乘结果中高 32 位与低 32 位的异或。 +​ 非线性激活层首先定义 $h_i = J_i\oplus J_{i+5}, 1\le i \le5$，其中 $J_i = W_i \times I_i$，$W_i \sim CS$，$I_i$ 是将输入的 320 比特等分成 10 份中的结果，长度为 32 比特，这里 $1 \le i \le 10$。32 位乘法定义为两数相乘结果中高 32 位与低 32 位的或运算。 ​ 然后，对这个结果的前 5 个 32 比特迭代重复 $N_r$ 次 $Cell_{5-8}$， @@ -236,7 +236,7 @@ $$ | 13 | Random Excursions Variant | 18/18$^1$ | 通过$^1$ | - | | 14 | Serial | 2/2$^1$ | 通过$^1$ | $m=\lfloor \log_2 n \rfloor -3$ | | 15 | Linear Complexity | 110/111 | 0.818179 | - | - +
Figure 4.2.1.1 NIST 测试结果
注： 1. 表示该检测度量有多个指标 @@ -261,6 +261,8 @@ $$ +
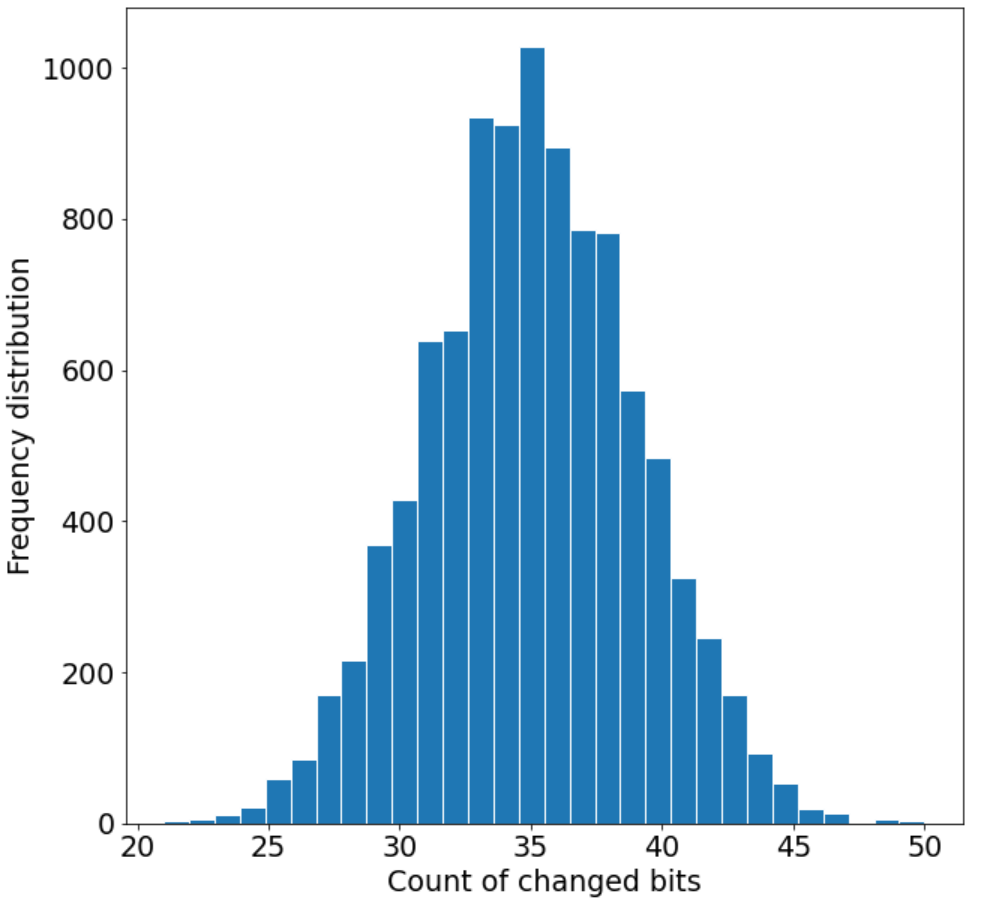Figure 4.2.2.1 Diffusion Test
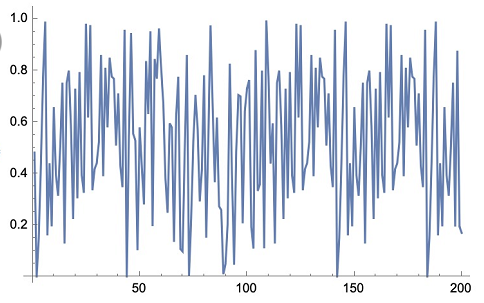+ 定量计算 1. 改变位数的最小值 $B_{\min }=\min \left(\left\{B_{i}\right\}_{i=1, \ldots, N}\right)$ @@ -279,6 +281,8 @@ $$ image-20220514222253677 +
Figure 4.2.3.1 DSTMap Result
+ ​ 我们混沌系统采用的发生函数 $\text{DSTMap}_Q$ 可以很好地起到生成均匀分布的数据的目的。我们这里对 STMap 做了实验，取 $\mu = 1, Q=0.3$，然后对输出函数 $\text{STMap}_{0.3}$ 做傅里叶变换后得到上图，可以看出数据具有较强的随机性，满足均匀分布的条件。 diff --git a/readme.pdf b/readme.pdf index 90e904c..f41e271 100644 Binary files a/readme.pdf and b/readme.pdf differ