Skip to content

Latest commit

 

History

History
590 lines (445 loc) · 27.4 KB

cutlass_cute_tutorial_en.md

File metadata and controls

590 lines (445 loc) · 27.4 KB
Raw

Reproduce Flash Attention with Cutlass Cute

Flash attention can be learned from the top-down (although I learned Cutlass from the bottom-up, but I feel that it should be learned from the top-down for quick mastery). With the help of Cutlass Cute, users can conveniently implement some functionalities, that is, some paradigms of CUDA programming:

  • CUDA Programming Paradigms: global mem -> share mem -> reg -> compute
    • Block Tiling:
      • aka reusing shared memory (smem), copying from global memory (gmem) to shared memory (smem)
    • Thread Tiling:
      • aka reusing registers (reg) and shared memory (smem), copying from shared memory (smem) to registers (reg)
    • Merging Memory Accesses, Vector Memory Accesses:
      • aka vector instructions, LDSM (Load Shared Memory), ldmatrix instructions
    • Warp Divergence:
      • aka warp load balancing, similarly to pipeline bubble issues
    • Bank Conflict Resolution: Swizzle
      • aka utilizing the multi-channel nature of memory
    • Double Buffering
      • aka the pipeline of loading and computing
    • ...

For those who need to learn from the bottom-up, I recommend reading the offical cute tutorial

Acknowledge

  • Base on offical flash attention, but rewrote it from scratch, eliminating many hidden tricks.
  • I simplified a lot of the engineering considerations of the original code, keeping only the core parts.
  • purely in CUDA, without considering the Pybind version: You can find it in the standalone folder.
  • It's been a while since I've worked on it, so you can directly use the Makefile to start learning.

flash attention three easy pieces

TODO: Briefly describe the essence of flash attention: flash attention three easy pieces

  • Online safe softmax
  • Fusion of two GEMMs
  • Mathematical principles of rescaling

Top-down Cute Flash Attention

When considering writing high-performance operators in pure CUDA without using Cutlass, here's how to approach it:

  1. Multi-dimensional block tiling:
    • Copy data from global memory to shared memory.
    • Reuse data in shared memory to reduce global memory accesses.
  2. Multi-dimensional thread tiling:
    • Copy data from shared memory to global memory.
    • Reuse data in registers.
  3. Further optimization.
  4. Use vector instruction asynchronous loading:
    • LDSM
    • ldmatrix
  5. Merge memory accesses.
  6. Resolve bank conflicts.
  7. Compute overlap pipelining: Copy data from global memory to shared memory while performing register-based GEMM calculations.

However, Cutlass Cute abstracts and encapsulates the code that originally needs to be handwritten for thread cooperation. For example, when cooperation is needed for copying, you can use make_tiled_copy to create a copy object, and when cooperation is needed for calculation, you can use TiledMMA<T> to create MMA (matrix multiply accumulate) objects for calculation.

Understanding MMA layout is sufficient to understand how threads cooperate. The following Tools section will introduce this.

Term Explanations

  • Naming Convention: tQgQ
    • You might be puzzled by the cute variable names, so it's necessary to explain.
    • For example, auto tQgQ = gmem_thr_copy_QKV.partition_S(gQ(_, _, 0)), t(to) indicates its purpose, here it's just an abstraction layer or Q itself, so it's directly named tQ. g indicates the position of the variable in global memory.
    • For instance, tSrQ, tSrK indicates it's used for Score computation in the register (reg), Q, K.
    • For example, tOrVt indicates it's used for the final output, V transposed in the register.
  • MNK Matrix Multiplication Notation
    • Two matrices need at least one dimension to be the same, K represents this common dimension.
    • A[M, K] @ B[N, K]
  • MMA (Matrix Multiply Accumulate)
    • Simply put, it's used to represent the scale of thread tiling, i.e., how many threads are used in a thread block and how they compute. Cute abstracts it as individual MMA objects.
  • MMA Description: Describes the instructions used for the underlying execution of D = AB + C, users can specify as needed.
    • Description format: DABC + MNK
    • DABC: Describes the register type, such as in SM75_16x8x8_F32F16F16F32_TN, F32F16F16F32 is the DABC description. It indicates that DABC registers are F32, F16, F16, F32.
    • MNK: Describes the scale of matrix multiplication, like in SM75_16x8x8_F32F16F16F32_TN, 16x8x8 indicates D[M, N] = A[M, K] * B[N, K] + C[M, N].
  • Tiled_MMA: Describes how multiple MMA_Atom cooperate to complete a large task.
    • AtomLayoutMNK: Repeats Atom in MNK direction inside a tile, repeated by multiple threads.
    • ValueLayoutMNK: Repeats calculations in MNK direction inside an Atom, repeated within a single thread.
  • BlockM
    • Granularity of block computation for Q.
  • BlockN
    • Granularity of block computation for KV.

Tools

  • Print MMA Layout

You can use this MMA layout printing script to print the layout. Usage is as follows: modify different MMA instructions like SM80_16x8x16_F32F16F16F32_TN for testing.

  {
    auto tiled_mma = make_tiled_mma(SM80_16x8x16_F32F16F16F32_TN{},
                                    Layout<Shape<_1,_1, _1>>{},  // AtomLayoutMNK
                                    Layout<Shape<_1,_2, _1>>{}   // ValLayoutMNK
    );
    print_mma_content("flash2: SM80_16x8x16_F32F16F16F32_TN", tiled_mma);
  }

Meaning of the image: T0, T1... represents threads, V0, V1 within T0 represent the data that thread T0 is responsible for.

  • Printing Tensors

You can directly use print_tensor and print_layout provided by Cute to print tensor data in the command line for debugging. For example:

// Convert a C pointer into cutlass Tensor
// with info like shape (M, K) and stride (K, 1)
const int M = 4;
const int K = 8;

Tensor A = make_tensor(c_host_ptr, make_shape(M, K), make_stride(K, 1));
cute::print_tensor(A);
cute::print_layout(A.layout());

/*
ptr[32b](0x7ffe79dcbbe0) o (4,8):(8,1):
    0    1    2    3    4    5    6    7
    8    9   10   11   12   13   14   15
   16   17   18   19   20   21   22   23
   24   25   26   27   28   29   30   31
(4,8):(8,1)
       0    1    2    3    4    5    6    7 
    +----+----+----+----+----+----+----+----+
 0  |  0 |  1 |  2 |  3 |  4 |  5 |  6 |  7 |
    +----+----+----+----+----+----+----+----+
 1  |  8 |  9 | 10 | 11 | 12 | 13 | 14 | 15 |
    +----+----+----+----+----+----+----+----+
 2  | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 |
    +----+----+----+----+----+----+----+----+
 3  | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 |
    +----+----+----+----+----+----+----+----+
*/

Use local_tile to print a tile (a slice of a tensor).

cute::print_tensor(A);
auto A00 = local_tile(A, make_tile(2, 2), make_coord(0, 0));
auto A01 = local_tile(A, make_tile(2, 2), make_coord(0, 1));
auto A10 = local_tile(A, make_tile(2, 2), make_coord(1, 0));
cute::print_tensor(A00);
cute::print_tensor(A01);
cute::print_tensor(A10);

/*

cute::print_tensor(A);
ptr[32b](0x7ffc3fe94680) o (4,8):(1,4):
    0    4    8   12   16   20   24   28
    1    5    9   13   17   21   25   29
    2    6   10   14   18   22   26   30
    3    7   11   15   19   23   27   31

cute::print_tensor(A00);
ptr[32b](0x7ffc3fe94680) o (2,2):(1,4):
    0    4
    1    5

cute::print_tensor(A01);
ptr[32b](0x7ffc3fe946a0) o (2,2):(1,4):
    8   12
    9   13

cute::print_tensor(A10);
ptr[32b](0x7ffc3fe94688) o (2,2):(1,4):
    2    6
    3    7

*/

Thread Model for Flash Attention

The single-threaded attention computation belike: q[seqlen, headdim] @ k[seqlen, headdim].T @ v[seqlen, headdim].

While multi-linear attention computation only requires slicing from the dimension of q (imagine in autoregressive scenarios, computing attention for one token at a time, here it's parallel computing for multiple "single" queries' attention), each thread is responsible for calculating single-head attention for BlockM tokens. That is,

If the input shape is [bs, head, seqlen, headdim], the total number of threads is bs x head x seqlen/BlockM, and each thread computes [BlockM, headdim] query attention calculation. This is parallel in both the bs x head dimension and the seqlen dimension.

Similarly, for each independent thread block, bs x head x seqlen/BlockM independent thread blocks are allocated to perform parallel computation for multiple tokens.

dim3 grid(ceil_div(params.seqlen, BlockM), params.bs * params.head, 1);

TODO: graph

2D Block Tiling

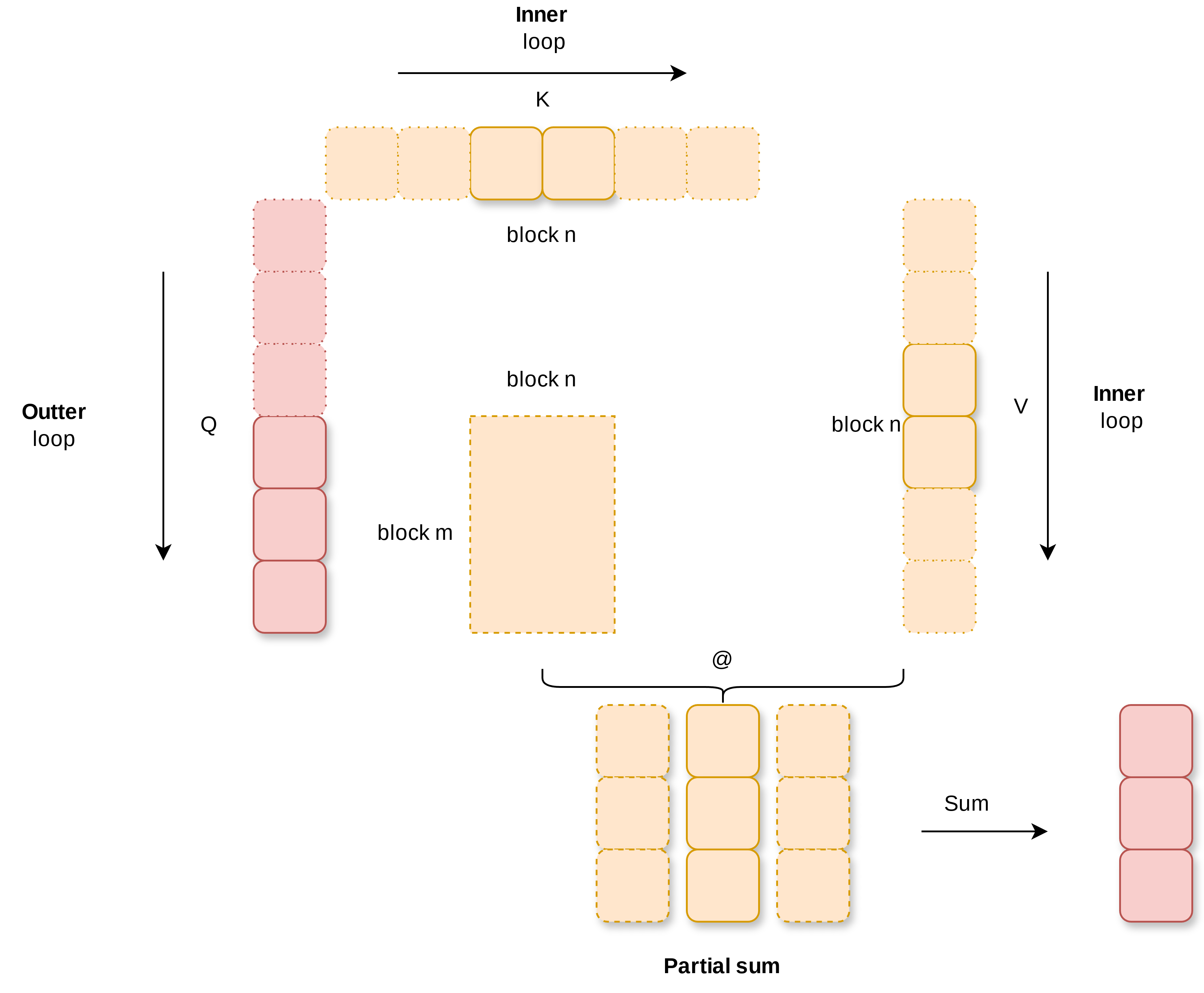
The computation process of Flash Attention 2 is illustrated in the following diagram. Q is calculated separately with K and V in inner loop order to obtain partial sums. Finally, the partial sums are accumulated to get an output of the same shape as Q. The pseudocode description (without considering the principles of online softmax and rescale) is as follows.

flash_attention_2():
    # outter loop
    parallel do q[NUM_BLOCK_M]:
        # inner loop
        for i in range(NUM_BLOCK_N):
            qk = q @ k[i].T
            score = online_softmax(qk)
            out += score @ v[i]
        rescale(out)

You may notice that the outer loop and inner loop are different from the widely circulated classic Flash Attention triangle diagram. This is because that diagram is from the Flash Attention 1 implementation.

Using Cute's API, we can quickly create blocks for q, k, v:

  • Use make_tensor() to wrap raw pointers into tensors for easier subsequent operations.
  • Use local_tile(tensor, tile, coord) to extract a group/one block from the tensor.
  • Create a Copy_Atom copy object to implement data copying from global memory to shared memory, which provides simple and easy-to-use multi-dimensional block tiling.

First, the make_tensor API is used to convert the passed raw pointer into a more convenient Tensor. Here, a complete seqlen x dim QKV object is created, making it convenient to use Cute's API for operations like q_slice[i++]. Don't worry about additional overhead from make_tensor because it doesn't create any.

  // dim3 grid(ceil_div(params.seqlen, BlockM), params.bs * params.head, 1);

  const int m_block = blockIdx.x;
  const int bs_head_offset = blockIdx.y * params.seqlen * params.dim;

  Tensor Q = make_tensor(
      make_gmem_ptr(reinterpret_cast<Element *>(params.q_ptr) + bs_head_offset),
      make_shape(params.seqlen, params.dim),
      make_stride(params.dim, Int<1>{}));
  Tensor K = make_tensor(
      make_gmem_ptr(reinterpret_cast<Element *>(params.k_ptr) + bs_head_offset),
      make_shape(params.seqlen, params.dim),
      make_stride(params.dim, Int<1>{}));
  Tensor V = make_tensor(
      make_gmem_ptr(reinterpret_cast<Element *>(params.v_ptr) + bs_head_offset),
      make_shape(params.seqlen, params.dim),
      make_stride(params.dim, Int<1>{}));

Load the QKV block corresponding to the thread block according to the block ID. local_tile(tensor, tile, coord) abstracts the tensor into an array composed of multiple tiles (in multiple dimensions), and then uses the coord to index and extract the required portion. Here, the Q block responsible for the current thread block is extracted, and the first KV block is extracted for subsequent "compute overlap pipelining" prefill.

Since the shape of Q here is seqlen, kHeadDim, splitting it into multiple [kBlockM, kHeadDim] blocks allows indexing with coord as [seqlen/kBlockM, kHeadDim/kHeadDim]. Extracting [m_block, _] is equivalent to indexing like [m_block, :] in Python. Here, the dimension indexed by m_block will be squeezed, while the dimension indexed by _ will be retained. So, the final shape is (kBlockM, kHeadDim, num_tile_n=1).

  // load q, k, v block
  // (kBlockM, kHeadDim, num_tile_n)
  Tensor gQ = local_tile(Q, make_tile(Int<kBlockM>{}, Int<kHeadDim>{}), make_coord(m_block, _));

  // (kBlockN, kHeadDim, num_tile_n)
  // NOTE: compute commu overlap pipeline load first q, k
  Tensor gK = local_tile(K, make_tile(Int<kBlockN>{}, Int<kHeadDim>{}), make_coord(0, _));
  Tensor gV = local_tile(V, make_tile(Int<kBlockN>{}, Int<kHeadDim>{}), make_coord(0, _));

Copying data from global memory to shared memory for multi-dimensional block tiling: Define an object for copying from global memory to shared memory, which reduces the need for users to directly use GPU instructions. The construction of the copy object will be discussed later, but in simple terms, it's configured using a config to specify the method of copying (asynchronous, vectorized).

  // Construct SMEM tensors.
  Tensor sQ = make_tensor(make_smem_ptr(shared_storage.smem_q.data()), SmemLayoutQ{});
  Tensor sK = make_tensor(make_smem_ptr(shared_storage.smem_k.data()), SmemLayoutK{});
  Tensor sV = make_tensor(make_smem_ptr(shared_storage.smem_v.data()), SmemLayoutV{});
  // Tensor for V Transpose; used in GEMM-II.
  Tensor sVt = make_tensor(make_smem_ptr(shared_storage.smem_v.data()), SmemLayoutVt{});
  Tensor sVtNoSwizzle = make_tensor(make_smem_ptr(shared_storage.smem_v.data()), SmemLayoutVtNoSwizzle{});

  // NOTE: define object of gmem -> smem copy, src, dst
  Tensor tQgQ = gmem_thr_copy_QKV.partition_S(gQ(_, _, 0));
  Tensor tQsQ = gmem_thr_copy_QKV.partition_D(sQ);
  Tensor tKgK = gmem_thr_copy_QKV.partition_S(gK(_, _, 0));
  Tensor tKsK = gmem_thr_copy_QKV.partition_D(sK);
  Tensor tVgV = gmem_thr_copy_QKV.partition_S(gV(_, _, 0));
  Tensor tVsV = gmem_thr_copy_QKV.partition_D(sV);

In this process, gmem_thr_copy_QKV.partition_S() creates the source address object for copying, while gmem_thr_copy_QKV.partition_D() creates the destination address object. Since we've fully utilized the second dimension when creating the block for gQ, the extraction with make_coord(m_block, _) results in only one element, so we directly use 0 to index it.

// tQgQ: tQ: used for (t) calculating Q. gQ: data in global memory
// tQsQ: tQ: used for (t) calculating Q. sQ: data in shared memory

Then, using the API, a multi-dimensional data copy can be achieved.

  // NOTE: gmem_tiled_copy_QKV为cute抽象出来的拷贝对象Copy_Atom, 表示用一组thread来做拷贝
  cute::copy(gmem_tiled_copy_QKV, tQgQ, tQsQ);
  // start async copy
  cute::cp_async_fence();

The construction method for the gmem_thr_copy_QKV copy object will be discussed later. You only need to pass in an asynchronous copy parameter and the scale layout to use vector instructions for asynchronous copying.

much simpler than manually writing GPU instructions for block tiling and various copies

2D Thread tiling

We are now entering the inner loop part of this section.

flash_attention_2():
    # outter loop
    parallel do q[NUM_BLOCK_M]:
        # inner loop
        for i in range(NUM_BLOCK_N):
            qk = q @ k[i].T
            score = online_softmax(qk)
            out += score @ v[i]
        rescale(out)

The overall process is as follows:

  1. pipeline prefill: load(q), load(k[0])
  2. pipeline start
  3. async_load(next(v)) && compute q @ k.T
  4. softmax(qk)
  5. async_load(next(k)) && compute qk @ v
  6. pipeline finish
  7. rescale

During the gemm calculation, multi-dimensional data is copied from shared memory to registers for thread tiling. Thread tiling allows reusing data already copied to registers, reducing the number of copies from shared memory to registers. As shown in the diagram below, when calculating the first row of the gemm, after BX0 and A0X calculations are completed, BX1 can directly use A0X already in registers without loading it again from shared memory to registers.

Looking at the implementation of multi-dimensional thread tiling from the perspective of gemm, we use cute::copy to copy the data tCsA from shared memory to registers tCrA, and then directly use cute::gemm to perform gemm calculation with multi-dimensional thread tiling. The specific layout of thread tiling can be viewed through printing mma.

template<typename Tensor0, typename Tensor1,
         typename Tensor2, typename Tensor3, typename Tensor4,
         typename TiledMma, typename TiledCopyA, typename TiledCopyB,
         typename ThrCopyA, typename ThrCopyB>
inline __device__ void gemm_smem(Tensor0 &acc, Tensor1 &tCrA, Tensor2 &tCrB, Tensor3 const& tCsA,
                            Tensor4 const& tCsB, TiledMma tiled_mma,
                            TiledCopyA smem_tiled_copy_A, TiledCopyB smem_tiled_copy_B,
                            ThrCopyA smem_thr_copy_A, ThrCopyB smem_thr_copy_B) {
    // NOTE: construct dst object of smem -> reg copy
    Tensor tCrA_copy_view = smem_thr_copy_A.retile_D(tCrA);
    Tensor tCrB_copy_view = smem_thr_copy_B.retile_D(tCrB);

    // NOTE: s -> reg
    cute::copy(smem_tiled_copy_A, tCsA(_, _, _0{}), tCrA_copy_view(_, _, _0{}));
    cute::copy(smem_tiled_copy_B, tCsB(_, _, _0{}), tCrB_copy_view(_, _, _0{}));
    #pragma unroll
    for (int i = 0; i < size<2>(tCrA); ++i) {
        if (i < size<2>(tCrA) - 1) {
            cute::copy(smem_tiled_copy_A, tCsA(_, _, i + 1), tCrA_copy_view(_, _, i + 1));
            cute::copy(smem_tiled_copy_B, tCsB(_, _, i + 1), tCrB_copy_view(_, _, i + 1));
        }
        cute::gemm(tiled_mma, tCrA(_, _, i), tCrB(_, _, i), acc);
    }
}

Before the for loop, we perform a cute::copy to construct a communication-compute overlap pipeline. This means doing smem->reg copy while performing gemm.

Returning to the Cutlass Flash Attention code, we use the API provided by Cute to construct the register objects needed for gemm. TODO: The specific construction method for the SmemCopyAtom copy object will be discussed later, but you only need to pass in an asynchronous copy parameter and the scale layout.

Use partition_fragment_A, partition_fragment_B, partition_fragment_C to create register objects, preparing for thread tiling: copying data from shared memory to registers, and performing matrix multiplication using data in registers.

    // NOTE: construct mma object in register
  // partition_fragment can create a object in register
  Tensor tSrQ  = thr_mma.partition_fragment_A(sQ); // (MMA,MMA_M,MMA_K)
  Tensor tSrK  = thr_mma.partition_fragment_B(sK); // (MMA,MMA_N,MMA_K)
  Tensor tOrVt  = thr_mma.partition_fragment_B(sVtNoSwizzle); // (MMA, MMA_K,MMA_N)
  // construct output accumulator
  Tensor rAccOut = partition_fragment_C(tiled_mma, Shape<Int<kBlockM>, Int<kHeadDim>>{});

  // construct copy object of smem -> reg
  auto smem_tiled_copy_Q = make_tiled_copy_A(typename Kernel_traits::SmemCopyAtom{}, tiled_mma);
  // select thread work by thread id 
  auto smem_thr_copy_Q = smem_tiled_copy_Q.get_thread_slice(tidx);
  // use partition_S to construct src object of Copy_Atom
  Tensor tSsQ = smem_thr_copy_Q.partition_S(sQ);
  ...

The inner loop code is as follows. Here, auto rAccScore = partition_fragment_C() is created to fuse two gemms: the gemm for score = [email protected] and the gemm for out = score @ v.

It's important to note the pitfalls of fusing two gemms. Because we need to fuse two gemms, the output of gemm-I, score = [email protected], needs to be used as the input of gemm-II, out = score @ v, so the C layout of gemm-I's output needs to match the A layout of gemm-II's input in order to be directly used. It's found through printing MMA instructions that SM80_16x8x16_F32F16F16F32_TN meets this requirement.

ColfaxResearch's implementation seems to handle this without considering this point, using rs_op_selector and ss_op_selector APIs to configure MMA. If someone knows how it works, please let me know.

/*
flash_attention_2():
    # outter loop
    parallel do q[NUM_BLOCK_M]:
        # inner loop
        for i in range(NUM_BLOCK_N):
            qk = q @ k[i].T
            score = online_softmax(qk)
            out += score @ v[i]
        rescale(out)
*/
  for (int nbi = n_block_min; nbi < n_block_max; nbi++) {
    auto rAccScore = partition_fragment_C(tiled_mma, make_shape(Int<kBlockM>{}, Int<kBlockN>{}));

    clear(rAccScore);

    // 等待Q, K的gmem -> smem拷贝完成, 即Q, K就绪
    // wait<0>表示等待还剩0个未完成
    flash::cp_async_wait<0>();
    __syncthreads();

    // gemm的同时异步加载V
    gV = local_tile(V, make_tile(Int<kBlockN>{}, Int<kHeadDim>{}), make_coord(nbi, _));
    tVgV = gmem_thr_copy_QKV.partition_S(gV(_, _, 0));
    // 异步加载V到smem
    flash::copy(gmem_tiled_copy_QKV, tVgV, tVsV);
    // 发起异步拷贝
    cute::cp_async_fence();

    // O = [email protected]
    // NOTE: 加载smem中的数据到reg再做gemm, **加载期间执行retile**
    flash::gemm_smem(rAccScore, tSrQ, tSrK, tSsQ, tSsK, tiled_mma, smem_tiled_copy_Q, smem_tiled_copy_K,
        smem_thr_copy_Q, smem_thr_copy_K
    );

    Tensor scores = make_tensor(rAccScore.data(), flash::convert_layout_acc_rowcol(rAccScore.layout()));

    // NOTE: 2. mask within N BLOCKs
    if (Is_causal ==  true && nbi * kBlockN >= seqlen_start) {
      flash::mask_within_nblock<kBlockM, kBlockN, kNWarps>(scores, m_block, nbi);
    }

    // NOTE: 等待V加载完成, 为下个K加载准备初始状态
    flash::cp_async_wait<0>();
    __syncthreads();

    // advance K
    if (nbi != n_block_max - 1) {
      gK = local_tile(K, make_tile(Int<kBlockN>{}, Int<kHeadDim>{}), make_coord(nbi + 1, _));
      tKgK = gmem_thr_copy_QKV.partition_S(gK(_, _, 0));
      flash::copy(gmem_tiled_copy_QKV, tKgK, tKsK);
      cute::cp_async_fence();
    }

    // 计算softmax
    // NOTE: rAccOut记录softmax后所有的分子
    nbi == 0 ? flash::softmax_rescale_o</*Is_first=*/true>(scores, scores_max, scores_sum, rAccOut, params.softmax_scale) :
      flash::softmax_rescale_o</*Is_first=*/false>(scores, scores_max, scores_sum, rAccOut, params.softmax_scale);

    // 实际执行QK @ V
    // (score AKA rAccScore): QK[M, N] @ V[N, dim]
    // NOTE: DABC: F32F16F16F32, convert D type(F32) to A type(F16)
    // TODO: convert_type目前写死
    Tensor rP = flash::convert_type_f32_to_f16(rAccScore);
    // NOTE: Convert from layout C to layout A
    Tensor tOrP = make_tensor(rP.data(), flash::convert_layout_rowcol_Aregs<TiledMMA>(scores.layout()));

    flash::gemm_A_in_regs(rAccOut, tOrP, tOrVt, tOsVt, tiled_mma, smem_tiled_copy_V, smem_thr_copy_V);
  }

The correspondence between pseudocode and code is as follows:

# inner loop
for nbi in range(NUM_BLOCK_N):
    # k[nbi]: gK = local_tile(K, make_tile(Int<kBlockN>{}, Int<kHeadDim>{}), make_coord(nbi + 1, _));
    qk = q @ k[nbi].T # flash::gemm_smem()
    score = online_softmax(qk) # softmax_rescale_o()
    # v[nbi]: gV = local_tile(V, make_tile(Int<kBlockN>{}, Int<kHeadDim>{}), make_coord(nbi, _));
    out += score @ v[nbi] # gemm_A_in_regs()

Communication Compute Overlap Pipeline

  • Asynchronous Copy

When creating the copy object from global memory to shared memory, use the SM80_CP_ASYNC_CACHEGLOBAL instruction to create an asynchronous Copy_Atom object.

using Gmem_copy_struct = std::conditional_t<
    Has_cp_async,
    SM80_CP_ASYNC_CACHEGLOBAL<cute::uint128_t>,
    DefaultCopy
>;
using GmemTiledCopyQKV = decltype(
    make_tiled_copy(Copy_Atom<Gmem_copy_struct, Element>{},
                    GmemLayoutAtom{},
                    Layout<Shape<_1, _8>>{}));  // Val layout, 8 vals per read
  • Pipeline

The pseudocode is as follows: when computing q@k, load v, and when computing qk@v, load the next iteration's required k. Currently, only double buffering is used to prefetch 1 set of kv. If prefetching multiple sets of kv each time, it's necessary to consider the impact of shared memory size on performance.

# inner loop
async_load(k[0]) # k[nbi]: gK = local_tile(K, make_tile(Int<kBlockN>{}, Int<kHeadDim>{}), make_coord(nbi + 1, _));
for nbi in range(NUM_BLOCK_N):
    # 加载v的同时计算q@k
    async_load(v[nbi]) # v[nbi]: gV = local_tile(V, make_tile(Int<kBlockN>{}, Int<kHeadDim>{}), make_coord(nbi, _));
    qk = q @ k[nbi].T # flash::gemm_smem()
    score = online_softmax(qk) # softmax_rescale_o()

    # 计算qk @ v的同时加载下一次迭代需要的k
    async_load(k[nbi]) # k[nbi]: gK = local_tile(K, make_tile(Int<kBlockN>{}, Int<kHeadDim>{}), make_coord(nbi + 1, _));
    out += score @ v[nbi] # gemm_A_in_regs()

Using this in Cutlass Cute is also straightforward. Once the asynchronous copy object is constructed, initiate the asynchronous copy.

    // gemm的同时异步加载V
    gV = local_tile(V, make_tile(Int<kBlockN>{}, Int<kHeadDim>{}), make_coord(nbi, _));
    tVgV = gmem_thr_copy_QKV.partition_S(gV(_, _, 0));
    // 异步加载V到smem
    flash::copy(gmem_tiled_copy_QKV, tVgV, tVsV);
    // 发起异步拷贝
    cute::cp_async_fence();

    // NOTE: 拷贝的同时执行gemm
    // O = [email protected]
    // NOTE: 加载smem中的数据到reg再做gemm, **加载期间执行retile**
    flash::gemm_smem(rAccScore, tSrQ, tSrK, tSsQ, tSsK, tiled_mma, smem_tiled_copy_Q, smem_tiled_copy_K,
        smem_thr_copy_Q, smem_thr_copy_K
    );

Other Details

  • Early Return in Causal Mode
    • Inter-block early exit
    • Intra-block Masking: Locating threads in MMA (Matrix Multiply and Accumulate)
  • Copying Results Back to Global Memory
    • Utilizing Shared Memory (smem), first copying from registers to smem and then from smem to global memory (gmem)
    • This allows the use of wider bit widths
  • Online Safe Softmax
  • Pybind and Template Expansion
    • The official implementation uses many templates, essentially:
      1. Enumerating all possible block partitioning strategies
      2. Writing a file for each configuration to accelerate compilation
      3. Writing a file for each template to fine-tune the best configuration
  • To integrate CPP code into Python, you can refer to this repository

Further details will be added later. Interested readers can first look into the source code comments.

Other Optimizations

  • Bank Conflict Avoding
    • Swizzling
    • Cutlass has encapsulated swizzle to solve bank conflicts. Use it when creating copy objects.
  • Transpose Optimization
    • Copy directly to the transposed destination address, avoiding the need to allocate new space
    • When creating copy objects, configure the layout to transpose the destination (dst) layout
  • High-performance Reduce Implementation
    • Optimizing warp divergence

TODO: Expand on details

A Little Bit Bottom-Up

For in-depth bottom-up understanding, refer to offical cute tutorials

TODO: Pick a few important points

Major Trick

  • Fusion of two gemms: gemm-I, gemm-II
    • The layout of input and output is critical: gemm-I's output C layout must match gemm-II's input A layout